Специфика временных рядов как источника данных в эконометрическом моделировании.

Под временным рядом ( динамическим рядом, или рядом динамики ) в экономике подразумевается последовательность наблюдений некоторого признака ( случайной величины ) У в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать y_t ( t= 1,2,….,n ), где n – число уровней.

В табл.6.1. приведены данные, отражающие спрос на некоторый товар за восьмилетний период (усл. ед), т.е. временной ряд спроса yt.

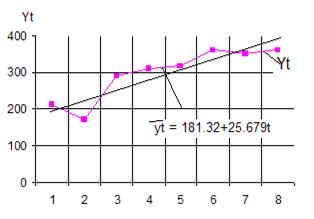
В качестве примера на рис.6.1. временной ряд y_t изображен графически.

В общем виде при исследовании экономического временного ряда y_t выделяются несколько составляющих:

y_t = u_t + v_t+ c_t+ e_t ( t = 1,2,…, n),

где u_t- тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т.е. длительную ( «вековую») тенденцию изменения признака ( например, рост населения, экономическое развитие, изменение структуры потребления и т.п.);

v_t- сезонная компонента, отражающая повторяемость экономических процессов в течение не очень длительного периода ( года, иногда месяца, недели и т.д. , например, объем продаж товаров или перевозок пассажиров в различные времена года );

c_t- циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов ( например, влияние волн экономической активности Кондратьева, демографических «ям», циклов солнечной активности и т.п.)

e_t- случайная компонента, отражающая влияние не поддающихся учету и регистрации случайных факторов.

Рис. 6.1.

Следует обратить внимание на то, что в отличие от e_t первые три составляющие (компоненты) u_t,v_t,c_t являются закономерными, неслучайными.

Важнейшие классической задачей при исследовании экономических рядов является выявление и статистическая оценка основой тенденции развития изучаемого процесса и отклонений от нее.

Отметим основные этапы анализа временных рядов:

. графическое представление и описание поведение временного ряда;

. выделение и удаление закономерных ( неслучайных ) составляющих временного ряда ( тренда, сезонных и циклических составляющих);

. сглаживание и фильтрация (удаление низко – или высокочастотных составляющих временного ряда);

. исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для ее описания;

. прогнозирование развития изучаемого процессов на основе имеющегося ряда;

. исследование взаимосвязи между различными временными рядами.

Среди наиболее распространенных методов анализа временных рядов выделим корреляционный и спектральный анализа, модели авторегрессии и скользящей средней. О некоторых из них речь пойдет ниже.

Если выборка y₁,y­₂,…..,y_i,…..,y_n рассматривается как одна из реализаций случайной величины У, временной ряд y₁,y­₂,…..,y_i,....,_,y_n рассматривается как одна из реализаций ( траекторий ) случайного процесса У_(t). Вместе с тем следует иметь в виду принципиальные отличия временного ряда y_t ( t = 1,2,..,n ) от последовательности наблюдений y₁,y­₂,….,y_n, образующих случайной выборку. Во первых, в отличие от элементов случайной выборки членов временного ряда, как правило, не являются статистически независимыми. Во-вторых, члены временного ряда не являются одинаково распределенными.