Автокорреляция в остатках, её измерение и интерпретация. Критерий Дарбина-Уотсона в оценке качества трендового уравнения регрессии.
Одна из важнейших задач (этапов) анализа временного (динамического) ряда, как отмечено выше, состоит в прогнозировании на его основе развития изучаемого процесса. При этом исходят из того, что тенденция развития, установленная в прошлом, может быть распространена (экстраполирована) на будущий период.
Задача ставиться так: имеется временной (динамический) ряд
yt (t=1,2,….,n) и требуется дать прогноз уровня этого ряда на момент n + t.
Выше, в §3.5, 4.2, 4.5, мы рассматривали точечный и интервальный прогноз значений зависимой переменной У, т.е. определение точечных и интервальных оценок У, полученных для парной и множественной регрессий для значений объясняющих переменных Х, расположенных вне пределов обследованного диапазона значений Х.
Если рассматривать временной ряд как регрессионную модель изучаемого признака по переменной «время», то к нему могут быть применены рассмотренные выше методы анализа. Следует, однако, вспомнить, что одна основных предпосылок регрессионного анализа состоит в том, что возмущения et (t = 1,2,…,n) представляют собой независимые случайные величины с математическим ожиданием (среднем значением), равным нулю. А при работе с временными рядами такое допущение оказывается во многих случаях неверным, (см. об этом гл.7.8).
В данной главе мы полагаем, что возмущения et (t = 1,2,…,n) удовлетворяют предпосылкам регрессионного анализа, т.е. условиям нормальной классической регрессионной модели (§3.4).
► Пример 6.4. По данным табл. 6.1 дать точечную и надежностью 0,95 интервальную оценки прогноза среднего и индивидуального значений спроса на некоторый товар на момент t = 9 (девятый год). (Полагаем, что тренд линейный, а возмущения удовлетворяют требованиям классической модели (см. дальше, пример 7.8.)).
Решение. Выше, в примере 6.1, получено уравнение регрессии ŷt = 181,32 + 25б679t, т.е. ежегодно спрос на товар увеличивался в среднем на 25,7 ед. Надо оценить условное математическое ожидание Мt=9(Y) = 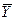 (9). Оценкой
(9). Оценкой 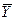 (9) является групповая средняя
(9) является групповая средняя
Ŷt=9 = 181,32 + 25,679 . 9 = 412,4 (ед.).
Найдем по формуле (3.26) оценку s2 дисперсии s2 (см. далее, табл. 7.1):
s2 = 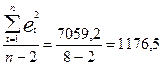
Вычислим оценку дисперсии групповой средней по формуле (3.33):
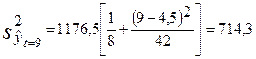 ;
;
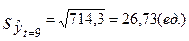
(здесь мы использовали данные, полученные в примере 6.2):
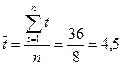 ;
;

По табл. II приложений t0,95;6 = 2,45. Теперь по формуле (3.34) интервальная оценка прогноза среднего значения спроса:
412,4 – 2,45. 26,73 £ ŷ(9) £ 412, 4 + 2,45. 26,73 ,
или 326,9 £ ŷ(9 £ 477,9 (ед.).
Для нахождения интервальной оценки прогноза индивидуального значения у*(9) вычислим дисперсию его оценки по формуле (3.35):

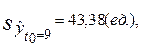
а зачем по формуле (3.36) – саму интервальную оценку для у*(9):
412, 4 - 2, 45 . 43, 38 £ у*(9) £ 412, 4 + 2, 45.43.38
или 305, 9 £ у*(9) £ 518,9 (ед.).
Итак, с надежностью 0,95 среднее значение спроса на товар на девятый год будет заключено от 346,9 до 477,9 (ед.), а его индивидуальное значение – от 305, 9 до 518, 9 (ед.).►
Прогноз развития изучаемого процесса на основе экстраполяции временных рядов может оказаться эффективным, как правило, в рамках краткосрочного, в крайнем случае, среднесрочного периода прогнозирования.
Для данного временного ряда далеко не всегда удается подобрать адекватнуюмодель, для которой ряд возмущений et будет удовлетворять основным предпосылкам регрессионного анализа. До сих пор мы рассматривали модели вида (6.7), в которых в качестве регрессора выступала переменная t – «время». В эконометрике достаточно широкое распространение получили и другие регрессионные модели, в которых регрессорами выступают лаговые переменные, т.е. переменные, влияние которых в эконометрической модели характеризуется некоторым запаздыванием. Еще одним отличием рассматриваемых в этом параграфе регрессионных моделей является то, что представленные в них объясняющие переменные являются величинами случайными. ( Подробнее об этих моделях см.гл.8)
Авторегрессионная модель р-го порядка (или модели AR (p)) имеет вид:
Уt = b0 + b1 Уt-1 + b2 Уt-2 +……+ bp Уt-p + et (t = 1,2,…,n),(6.11)
где b0 , b1,……, bp – некоторые константы.
Она описывает изучаемый процесса в момент t в зависимости от его значений в предыдущий период t – 1, t -2, …,t – p.
Если исследуемый процесс уt в момент t определяется его значениями только в предшествующий период t – 1, то рассматривают авторегрессионную модель 1–го порядка (или модель AR (1) – Марковский случайный процесс):
Уt = b0 + b1 Уt-1 + et ,, (t = 1,2,…,n). (6.12)
► Пример 6.5. В таблице представлены данные, отражающие динамику курса акций некоторой компании (ден. ед.):
Таблица 6.2
| t | |||||||||||
| Уt | |||||||||||
| t | |||||||||||
| Уt |
Используя авторегрессионную модель 1-го порядка, дать точечный и интервальный прогноз среднего и индивидуального значений курса акций момент t = 23, т.е. на глубину один интервал.
Решение. Попытка подобрать данному временному ряду адекватную модель вида (6.7) с линейным или полиномиальным трендом оказывается бесполезной.
В соответствии с условием применим авторегрессионную модель (6.12). Получим (аналогично примеру 6.2)
Ŷt = 284,0 + 0,7503yt-1. (6.13)
Найденное уравнение регрессии значимо на 5%-ном уровне по F – критерию, так как фактически наблюдаемое значение статистики F = 24,31 > F0,05;1;19 = 4,35. Можно показать (например, с помощью критерию Дарбина – Уотсона) (см. далее, § 7.7), что возмущения (ошибки) et в данной модели удовлетворяют условиям классической модели и для проведения прогноза могут быть использованы уже изученные нами методы.
Вычисления, аналогичные примеру 6.3, дают точный прогноз по уравнению(6.13):
Ŷt=23 = 284,0 +0, 7503. 1213 = 1194,1
и интервальный на уровне значимости 0,05 для среднего или индивидуального значений –
1046,6 £ 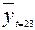 £ 1341,6 ; 879,1 £
£ 1341,6 ; 879,1 £ 
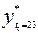 £ 1509,1.
£ 1509,1.
Итак, с надежностью 0,95 среднее значение курса акций данной компании на момент t= 23 будет заключено в пределах от 1046,6 до 1341,6 (ден. ед.), а его индивидуальное значение – от 879,1 до 1509,1 (ден. ед.).►
Наряду с авторегрессионным моделями временных рядов в эконометрике рассматриваются также модели скользящей средней, в которой моделируемая величина задается линейной функцией от возмущений (ошибок) в предыдущие моменты времени.
Модель скользящей средней q-го порядка (или модель MA (q)), имеет вид:
Yt = et + g1 et-1 + g2 et-2 +…..+ gq et-q (6.14)
В эконометрике используются также комбинированные модели временных рядов АR и МА.
Авторегрессионная модель скользящей средней порядков p и q соответственно (или модель ARMA (p,q) имеет вид:
Уt = b0 + b1 Уt-1 +…..+bp Уt-p +et + g1 et-1 + g2 et-2 +…..+ gq et-q . (6.15)
В заключение этой главы отметим, что использование соответствующих
авторегрессионных моделей для прогнозирования экономических показателей, т.е. автопрогноз на базе рассмотренных моделей, может оказаться весьма эффективным (как правило в краткосрочной перспективе).
Упражнения
В примерах 6.6 – 6.8 имеются следующие данные об урожайности озимой пшеницы yt (ц/га) за 10 лет:
| t | ||||||||||
| yt | 16,3 | 20,2 | 17,1 | 7,7 | 15,3 | 16,3 | 19,9 | 14,4 | 8,7 | 20,7 |
6.6. Найти среднее значение, среднее квадратическое отклонение и коэффициенты автокорреляции (для лагов t = 1;2) временного ряда.
6.7. Найти уравнение тренда временного ряда yt, полагая, что он линейный, и проверить его значимость на уровне 0,05.
6.8. Провести сглаживание временного ряда yt методом скользящих средних, используя простую среднюю арифметическую интервалом сглаживания:а) m = 3; m = 5.
6.9. В таблице представлены данные, отражающие динамику роста доходов на душу населения yt (ден. ед.) за восьмилетний период:
| t | ||||||||
| yt |
Полагая, что тренд линейный и условия классической модели выполнены:
а) найти уравнение тренда и оценить его значимость на уровне 0,05;
б) дать точечный и с надежностью 0,95 интервальный прогноза среднего и индивидуального значений доходов на девятый год.
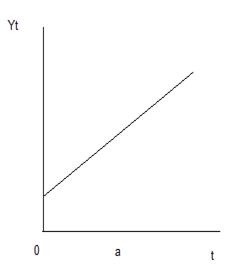
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы. Во – первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель.
Однако в совокупности они формируют его возрастающую или убывающую временной ряд, содержащий возрастающую тенденцию.
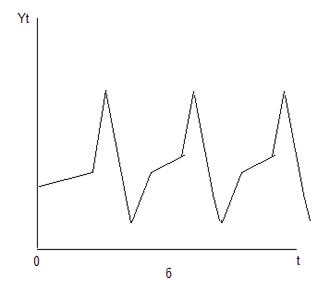
Во–вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Этих колебания могу носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний, уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктура рынка, а также с фазой-бизнес цикла, в которой находится экономика страны. На рис.5.1.б) представлен гипотетический временной ряд, содержащий только сезонную компоненту.
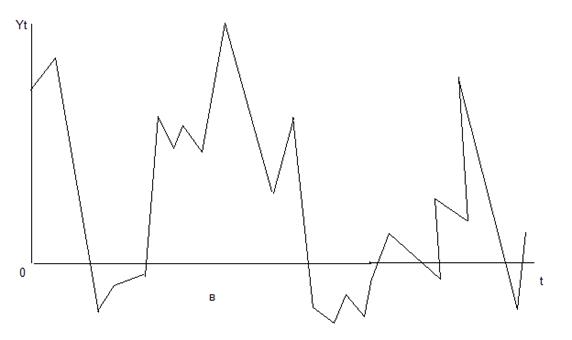
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты. Пример ряда, содержащего только случайно компоненту, приведен на рис.5.1.в).
Очевидно, что реальные данные не следуют целиком и полностью из каких-либо описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы
использования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
Дата добавления: 2016-05-16; просмотров: 3301;
