Автокорреляция, ее природа. Тестирование автокорреляции – метод Дарбина-Уотсона.
Одна из предпосылок метода наименьших квадратов – это независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Если эта предпосылка нарушается, то имеем место с автокорреляцией. Автокорреляцией называется зависимость между значениями одной выборки с запаздыванием на один лаг. Например, если между значениями одной выборки 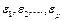 и
и 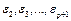 есть зависимость, то имеем место с автокорреляцией. Автокорреляция может быть, как положительной, так и отрицательной. Автокорреляция может возникнуть по многим причинам: во-первых, ее вызывает инерционность экономических процессов и, как следствие, зависимость между данными во временных рядах; во-вторых, некорректно специфицированные модели, манипуляции с данными, введение лаговых переменных.
есть зависимость, то имеем место с автокорреляцией. Автокорреляция может быть, как положительной, так и отрицательной. Автокорреляция может возникнуть по многим причинам: во-первых, ее вызывает инерционность экономических процессов и, как следствие, зависимость между данными во временных рядах; во-вторых, некорректно специфицированные модели, манипуляции с данными, введение лаговых переменных.
Наиболее известный способ обнаружения автокорреляции – это тест Дарбина-Уотсона.
Пусть 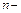 число наблюдений,
число наблюдений, 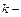 число факторов модели,
число факторов модели, 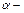 уровень значимости. По таблицам распределения Дарбина-Уотсона находим числа
уровень значимости. По таблицам распределения Дарбина-Уотсона находим числа 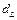 и
и 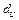 Рассчитываем значение
Рассчитываем значение 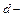 статистики по формуле
статистики по формуле
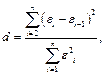
где 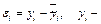 эмпирические данные,
эмпирические данные, 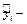 теоретические значения, полученные с использованием уравнения регрессии
теоретические значения, полученные с использованием уравнения регрессии 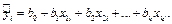
Доказано, что 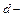 значения статистики Дарбина-Уотсона находятся в интервале от 0 до 4. Если рассчитанное значение
значения статистики Дарбина-Уотсона находятся в интервале от 0 до 4. Если рассчитанное значение 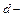 статистики находится в интервале от 0 до
статистики находится в интервале от 0 до 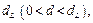 то это свидетельствует о наличии положительной автокорреляции. Если значение
то это свидетельствует о наличии положительной автокорреляции. Если значение 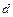 попадает в зону неопределенности, т.е. принимает значения
попадает в зону неопределенности, т.е. принимает значения 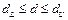 или
или 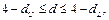 то мы не можем сделать вывод ни о наличии, ни об отсутствии автокорреляции. Если
то мы не можем сделать вывод ни о наличии, ни об отсутствии автокорреляции. Если 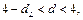 то имеем отрицательную автокорреляцию. Наконец, если
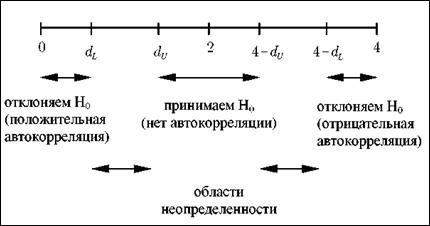
то имеем отрицательную автокорреляцию. Наконец, если 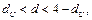 то автокорреляция отсутствует. Все эти случаи проиллюстрированы на рисунке.
то автокорреляция отсутствует. Все эти случаи проиллюстрированы на рисунке.
|
Рис. 3.2 Зоны автокорреляционной связи по критерию Дарбина-
Уотсона.
При автокорреляции нежелательна оценка параметров уравнения методом наименьших квадратов, т.к. она приводит к неэффективным оценкам и невозможности применения 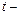 и
и 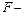 тестов.
тестов.
Если автокорреляция вызвана отсутствием в модели важной объясняющей переменной, то нужно попытаться определить этот фактор и включить его в модель. Также можно попытаться изменить форму зависимости. Но если все разумные процедуры изменения спецификации модели исчерпаны, а автокорреляция имеет место, то можно воспользоваться авторегрессионным преобразованием.
Для простоты ограничимся моделью парной линейной регрессии и авторегрессионной схемой первого порядка 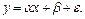
Вместо переменных 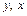 рассмотрим переменные
рассмотрим переменные 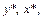 значения которых вычисляются по формулам
значения которых вычисляются по формулам
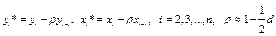 (3.8)
(3.8)
Поправки Прайса-Винстена:
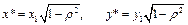 .
.
Положим 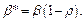 Тогда по таблице значений переменных
Тогда по таблице значений переменных 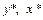 оцениваются коэффициенты уравнения
оцениваются коэффициенты уравнения 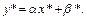 Затем получаем
Затем получаем 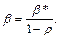
Пример.Оценить коэффициенты уравнения 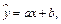 где значения переменных
где значения переменных 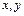 - первые два столбца таблицы 3.1.
- первые два столбца таблицы 3.1.
На основании критерия Дарбина-Уотсона гипотеза об отсутствии автокорреляции не может быть не принята, ни опровергнута: 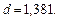
Применим авторегрессионную схему первого порядка
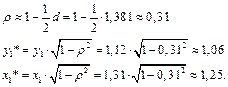
Остальные значения вычисляем по формулам (3.8). Заполняем третий и четвертый столбцы таблицы (округляем до двух цифр после запятой).
Теперь по методу наименьших квадратов для переменных 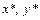 находим коэффициенты уравнения
находим коэффициенты уравнения
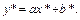 (3.9)
(3.9)
Таблица 3.1
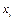
| 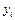
| 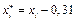
| 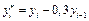
| 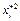
| 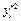
| 
|
| 1,31 2,21 1,37 1,87 1,53 2,14 2,26 1,31 1,76 1,28 1,88 1,46 2,22 1,75 1,29 1,99 2,27 1,29 2,28 1,84 2,05 2,17 1,98 1,28 1,29 | 1,12 -0,36 1,41 0,79 0,87 -0,11 0,10 1,63 -0,07 0,93 0,44 1,24 0,09 0,77 1,64 0,54 -0,30 1,43 -0,07 0,58 0,22 0,11 0,25 2,00 1,67 | 1,25 1,80 0,68 1,45 0,95 1,67 1,60 0,61 1,35 0,73 1,48 0,88 1,77 1,06 0,75 1,59 1,65 0,59 1,88 1,13 1,48 1,53 1,31 0,67 0,89 | 1,06 -0,71 1,52 0,35 0,63 -0,38 0,13 1,60 -0,58 0,95 0,15 1,10 -0,29 0,74 1,40 0,03 -0,47 1,52 -0,51 0,60 0,04 0,04 0,22 1,92 1,05 | 1,5625 3,2400 0,4624 2,1025 0,9025 2,7889 2,5600 0,3721 1,8225 0,5329 2,1904 0,7744 3,1329 1,1236 0,5625 2,5281 2,7225 0,3481 3,5344 1,2769 2,1904 2,3409 1,7161 0,4489 0,7921 | 1,1236 0,5041 2,3104 0,1225 0,3969 0,1444 0,0169 2,5600 0,3364 0,9025 0,0225 1,2100 0,0841 0,5476 1,9600 0,0009 0,2209 2,3104 0,2601 0,3600 0,0016 0,0016 0,0484 3,6864 1,1025 | 1,3250 -1,2780 1,0336 0,5075 0,5985 -0,6346 0,2080 0,9760 -0,7830 0,9635 0,2220 0,9680 -0,5133 0,7844 1,0500 0,0477 -0,7755 0,8968 -0,9588 0,6780 0,0592 0,0612 0,2882 1,2864 0,9345 |
 30,76 30,76
| 30,76 | 12,11 | 42,028 | 20,234 | 8,8253 |
Коэффициенты уравнения (3.9) находим по формулам (1.3), (1.5).
Вычислим средние и дисперсии:
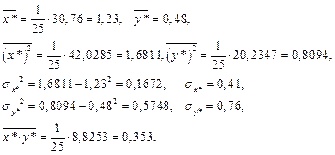 Вычислим коэффициенты
Вычислим коэффициенты 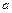 и
и 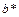 :
:
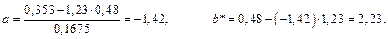
Коэффициент 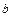 находим по формуле:
находим по формуле:
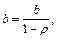 т.е.
т.е. 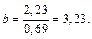
Для переменных 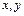 уравнение регрессии будет иметь вид:
уравнение регрессии будет иметь вид:
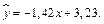
Дата добавления: 2016-05-11; просмотров: 2884;
