Производственная функция Кобба-Дугласа.
Наряду с линейными уравнениями множественной регрессии в экономике широко используются и нелинейные уравнения. Чаще всего эти уравнения с помощью соответствующих замен пытаются свести к линейным.
В экономике широко используется производственная функция Кобба-Дугласа, которая имеет вид:
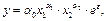 (3.9)
(3.9)
где 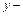 выпуск продукции;
выпуск продукции; 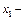 затраты труда;
затраты труда; 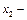 затраты капитала;
затраты капитала; 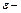 случайная величина.
случайная величина.
Коэффициенты 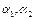 имеют конкретный экономический смысл. Действительно, найдем частные коэффициенты эластичности по переменным
имеют конкретный экономический смысл. Действительно, найдем частные коэффициенты эластичности по переменным 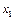 и
и 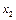 :
:
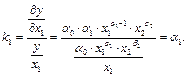
Аналогично 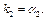 Параметр
Параметр 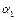 является коэффициентом эластичности выпуска от затрат труда. Он показывает, на сколько процентов изменится выпуск продукции, если затраты труда изменятся на один процент при условии, что затраты капитала останутся баз изменений. Параметр
является коэффициентом эластичности выпуска от затрат труда. Он показывает, на сколько процентов изменится выпуск продукции, если затраты труда изменятся на один процент при условии, что затраты капитала останутся баз изменений. Параметр 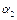 является коэффициентом эластичности выпуска от затрат капитала при условии, что затраты труда останутся без изменений.
является коэффициентом эластичности выпуска от затрат капитала при условии, что затраты труда останутся без изменений.
Сумма параметров 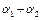 описывает масштаб производства. Если эта сумма равна 1, то имеет место постоянный масштаб производства; если она меньше 1, то имеет место спад производства, при котором увеличение фактора приводит к спаду выпуска продукции. Если
описывает масштаб производства. Если эта сумма равна 1, то имеет место постоянный масштаб производства; если она меньше 1, то имеет место спад производства, при котором увеличение фактора приводит к спаду выпуска продукции. Если 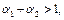 то, наоборот, наблюдается рост производства; увеличение значений факторов, например в
то, наоборот, наблюдается рост производства; увеличение значений факторов, например в 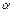 раз , приводит к увеличению выпуска продукции больше, чем в
раз , приводит к увеличению выпуска продукции больше, чем в 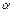 раз.
раз.
Модель (3.9) является нелинейной, однако логарифмируя это уравнение легко свести его к линейной регрессионной модели:
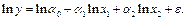
Обозначив 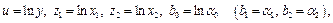 получим линейное уравнение регрессии вида (3.10).
получим линейное уравнение регрессии вида (3.10).
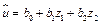 (3.10)
(3.10)
Теперь, используя, описанные выше методы для линейного множественного уравнения регрессии, найдем коэффициенты 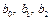 , а затем запишем уравнение в виде (3.9).
, а затем запишем уравнение в виде (3.9).
Рассмотрим конкретный пример (см. 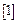 , стр. 220). Имеются данные об деревообрабатывающем секторе Украины (табл. 3.2)
, стр. 220). Имеются данные об деревообрабатывающем секторе Украины (табл. 3.2)
Таблица 3.2
| Год | Объем продукции (млн. у.е.) | Затраты труда (млн. дней) | Затраты капитала (млн. у.е.) |
| 12767,5 16347,1 19542,7 21075,9 23052,0 26128,2 29563,7 33376,6 38354,3 46868,3 54308,0 | 375,2 402,5 478,0 553,4 616,7 695,7 790,3 816,0 848,8 873,1 999,2 |
Дальнейшие вычисления сведем в таблицу 3.3. Первые три столбца – объем продукции, затраты труда, затраты капитала 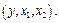 Следующие три столбца получаем логарифмирование:
Следующие три столбца получаем логарифмирование: 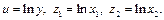
Уравнение регрессии будет иметь вид
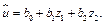
Найдем среднее и дисперсии для 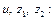
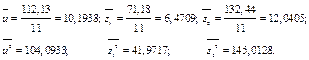
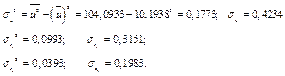
Найдем выборочные коэффициенты корреляции. Для этого сначала вычислим средние произведений:
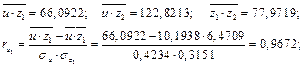
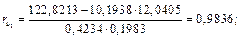
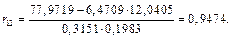
Система уравнений для определения коэффициентов 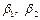 в стандартом масштабе принимает вид
в стандартом масштабе принимает вид
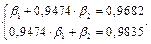
Решая эту систему, находим 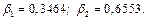 Коэффициенты
Коэффициенты 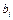 уравнения (3.9) в натуральном масштабе находим по формуле
уравнения (3.9) в натуральном масштабе находим по формуле 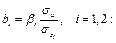
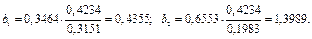 Коэффициент
Коэффициент 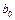 находим по формуле
находим по формуле
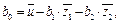 т.е.
т.е.
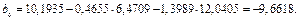
Уравнение (3.9) принимает вид
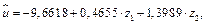
а производственная функция Кобба-Дугласа будет иметь вид
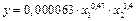 (3.10)
(3.10)
Из модели (3.10) видим, что в деревообрабатывающем секторе коэффициенты выпуска продукции от труда и капитала соответственно равняются 0,47 и 1,4, т.е., если затраты труда при неизменном значении капитала увеличились на 1% , то выпуск продукции увеличился на 0,47%.
Увеличение на 1% затрат капитала, когда затраты труда остались неизменными, приводит к увеличению на 1,4% выпуска продукции. Сумма параметров 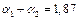 свидетельствует о расширении масштаба деревообрабатывающего производства.
свидетельствует о расширении масштаба деревообрабатывающего производства.
Таблица 3.3

| 
| 
| 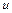
| 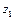
| 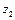
| 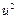
| 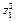
| 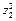
| 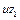
| 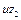
| 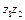
| |
| 12767,5 | 375,2 | 9,4547 | 5,9275 | 11,7862 | 89,3906 | 35,1348 | 138,9147 | 56,0421 | 111,4346 | 69,8623 | ||
| 16347,1 | 402,5 | 9,7018 | 5,9977 | 11,8076 | 94,1250 | 35,9723 | 139,4191 | 58,1885 | 114,5549 | 70,8183 | ||
| 19542,7 | 478,0 | 9,8804 | 6,1696 | 11,8425 | 97,6215 | 38,0641 | 140,2449 | 60,9580 | 117,0082 | 73,0636 | ||
| 21075,9 | 553,4 | 9,9559 | 6,3161 | 11,8944 | 99,1197 | 39,8929 | 141,4777 | 62,8822 | 118,4197 | 75,1262 | ||
| 23075,0 | 616,7 | 10,0465 | 6,4244 | 11,9428 | 100,9323 | 41,2727 | 142,6316 | 64,5426 | 119,9839 | 76,7254 | ||
| 26128,2 | 695,7 | 10,1708 | 6,5449 | 12,0124 | 103,4446 | 42,8360 | 144,2974 | 66,5669 | 122,1752 | 78,6201 | ||
| 29563,7 | 790,3 | 10,2943 | 6,6724 | 12,0831 | 105,9727 | 44,5211 | 146,0022 | 68,6878 | 124,3875 | 80,6237 | ||
| 33376,6 | 816,0 | 10,4156 | 6,7044 | 12,1450 | 108,4849 | 44,9492 | 147,5004 | 69,8306 | 126,4973 | 81,4249 | ||
| 38354,3 | 848,8 | 10,5546 | 6,7438 | 12,2349 | 111,4000 | 45,4792 | 149,6918 | 71,1785 | 129,1343 | 82,5097 | ||
| 46868,3 | 873,1 | 10,7551 | 6,7721 | 12,3093 | 115,6721 | 45,8607 | 151,5188 | 72,8341 | 132,3877 | 83,3592 | ||
| 54308,0 | 999,2 | 10,9024 | 6,9070 | 12,3872 | 118,8629 | 47,7060 | 153,4429 | 75,3026 | 135,0506 | 85,5579 | ||
| Суммы | 112,13 | 71,18 | 132,45 | 1145,026 | 461,69 | 1595,14 | 727,0137 | 1351,0338 | 857,6913 | |||
| Средние | 10,1938 | 6,4709 | 12,0405 | 104,0933 | 41,9717 | 145,0128 | 66,0922 | 122,8213 | 77,9719 | |||
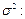
| 0,1793 | 0,0993 | 0,0393 | |||||||||
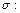
| 0,4234 | 0,3151 | 0,1983 |
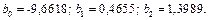
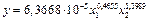
Дата добавления: 2016-05-11; просмотров: 968;
