Частные коэффициенты корреляции. Проверка их значимости. Отбор существенных факторов.
При построении экономической модели одной из проблем выбора является вопрос об определении существенности влияния на показатель отдельных факторов. Есть два противоположных критерия для выбора окончательной модели регрессионного анализа.
1. Если мы хотим сделать модель полезной для прогноза, то должны включить как можно больше факторов, чтобы значение прогнозируемой величины было как можно более точным.
2. Поскольку получение информации при большом количестве переменных требует больших затрат, то следует стремиться к тому, чтобы модель включала, по возможности, меньше факторов.
Компромиссом между этими крайностями является то, что называется выбором «наилучшего» уравнения регрессии. Существует большое количество методов построения регрессионной модели, наиболее известными из которых являются:
a. метод всех возможных регрессий;
b. метод исключений;
c. пошаговый регрессионный анализ;
d. гребневая регрессия;
e. регрессия на главные компоненты и др.
Метод всех возможных регрессий исторически является первым методом построения регрессионной модели. Он очень громоздкий и может быть реализован только на ЭВМ.
Поскольку для каждого фактора 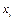 есть две возможности – входить или не входить в уравнение, то всего будет
есть две возможности – входить или не входить в уравнение, то всего будет 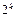 уравнений (
уравнений ( 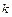 - количество факторов). Каждое уравнение потом оценивается с помощью коэффициента детерминации
- количество факторов). Каждое уравнение потом оценивается с помощью коэффициента детерминации 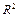 и проверки на адекватность.
и проверки на адекватность.
Рассмотрим идею этого метода на примере линейной регрессионной модели с 4-мя факторами: 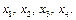 Все возможные уравнения разобьем на 5 серий:
Все возможные уравнения разобьем на 5 серий:
I серия моделей включает только один случай:
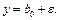
II серия – все возможные однофакторные уравнения;
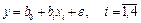
Ш серия – все возможные двухфакторные модели;
IY серия – все возможные трехфакторные модели;
Y серя – четырехфакторная модель:
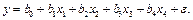
После того, как получены все модели по сериям, проранжируем их внутри каждой серии по значениям 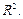 Выберем модели, которые имеют наибольшее значение коэффициента детерминации
Выберем модели, которые имеют наибольшее значение коэффициента детерминации 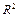 в каждой серии, и проанализируем есть ли какая-то закономерность в переменных, входящих в каждое из «наилучших» уравнений. Выбор окончательного уравнения в какой-то степени субъективная оценка исследователя. В случае, когда тяжело сделать такой выбор, можно рассмотреть дополнительный критерий -
в каждой серии, и проанализируем есть ли какая-то закономерность в переменных, входящих в каждое из «наилучших» уравнений. Выбор окончательного уравнения в какой-то степени субъективная оценка исследователя. В случае, когда тяжело сделать такой выбор, можно рассмотреть дополнительный критерий - 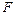 -критерий Фишера.
-критерий Фишера.
Анализ всех возможных уравнений регрессий – очень громоздкая и ненадежная процедура. Метод исключений более экономичный, чем метод всех регрессий. На первом этапе составляют уравнение регрессии, в которое включают все факторы, которые входят в модель. Затем вычисляется величина частичного 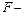 критерия для каждого фактора (понятие частичного
критерия для каждого фактора (понятие частичного 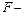 критерия поясним позже).Находим наименьшее значение частичного
критерия поясним позже).Находим наименьшее значение частичного 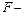 критерия, которое обозначим
критерия, которое обозначим 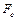 , и находим
, и находим 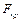 . Если
. Если 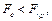 то соответствующий фактор исключается из уравнения. После этого составляется уравнение регрессии без отброшенного фактора и процедура проверки существенности факторов повторяется. Если
то соответствующий фактор исключается из уравнения. После этого составляется уравнение регрессии без отброшенного фактора и процедура проверки существенности факторов повторяется. Если 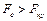 , то уравнение регрессии сохраняется.
, то уравнение регрессии сохраняется.
Пошаговый регрессионный метод действует в обратном порядке по сравнению с методом исключений. Факторы по очереди включаются в модель до тех пор, пока она не станет удовлетворительной. Сначала выбирается фактор 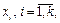 который имеет наибольший коэффициент корреляции с
который имеет наибольший коэффициент корреляции с  (пусть это будет переменная
(пусть это будет переменная 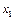 ). Строится уравнение регрессии с одной независимой переменной
). Строится уравнение регрессии с одной независимой переменной 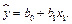 После этого проверяется значима ли эта замена по частичному
После этого проверяется значима ли эта замена по частичному 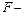 критерию. Если нет, то принимаем
критерию. Если нет, то принимаем 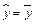 и процесс построения модели заканчиваем. Если да , то ищем следующую переменную, которая имеет наибольший коэффициент корреляции с
и процесс построения модели заканчиваем. Если да , то ищем следующую переменную, которая имеет наибольший коэффициент корреляции с  . Пусть это будет
. Пусть это будет 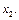 Получаем новое уравнение регрессии:
Получаем новое уравнение регрессии: 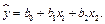 Анализируется изменение коэффициента корреляции
Анализируется изменение коэффициента корреляции 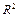 и рассчитываются частичные
и рассчитываются частичные 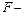 критерии для каждого из факторов. Среди них выбирается наименьшее его значение
критерии для каждого из факторов. Среди них выбирается наименьшее его значение 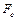 и сравнивается с
и сравнивается с 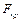 . В зависимости от результатов проверки переменная или остается в модели, или исключается. Может случиться так, что фактором, который на каком-то этапе был не наихудшим, потом из модели исключается. После этого модель пересчитывается в зависимости от факторов, которые остались. Процесс построения модели заканчивается, если ни один фактор, который находится в модели, не удается исключить, а новый претендент на включение не отвечает частичному
. В зависимости от результатов проверки переменная или остается в модели, или исключается. Может случиться так, что фактором, который на каком-то этапе был не наихудшим, потом из модели исключается. После этого модель пересчитывается в зависимости от факторов, которые остались. Процесс построения модели заканчивается, если ни один фактор, который находится в модели, не удается исключить, а новый претендент на включение не отвечает частичному 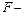 критерию.
критерию.
Пошаговый метод является наиболее распространенным на практике. Иногда применяются модификации указанных выше методов.
Частичный коэффициент корреляции может быть определен по формуле:
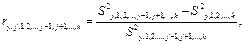
где 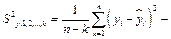 остаточная дисперсия для уравнения регрессии, содержащем
остаточная дисперсия для уравнения регрессии, содержащем 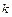 факторов
факторов 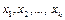 , а
, а 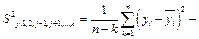 остаточная дисперсия для уравнения регрессии, содержащего факторы
остаточная дисперсия для уравнения регрессии, содержащего факторы 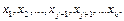
Частный коэффициент корреляции можно вычислить и по другой формуле:
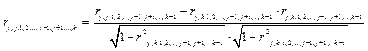 .
.
Например, частный коэффициент первого порядка
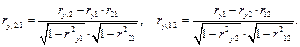
Частный коэффициент второго порядка
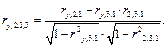
Частный коэффициент третьего порядка
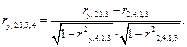
Все частные коэффициенты любого порядка выражаются через коэффициенты нулевого порядка. При этом частный коэффициент корреляции, например 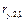 , оценивает силу линейной корреляционной зависимости между
, оценивает силу линейной корреляционной зависимости между  и
и 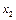 , когда
, когда 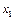 остается постоянным, и оценивается влияние на
остается постоянным, и оценивается влияние на  изменения
изменения 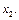 Частный коэффициент
Частный коэффициент 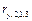 оценивает силу линейной корреляционной связи между
оценивает силу линейной корреляционной связи между  и
и 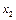 , когда
, когда 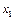 и
и 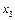 остаются постоянными, и оценивается влияние на
остаются постоянными, и оценивается влияние на  исключительно изменением
исключительно изменением 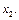
Ошибка выборки для частного коэффициента корреляции 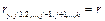 может быть определена по формуле
может быть определена по формуле
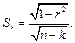
Существенность частного коэффициента корреляции проверяется по 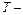 критерию
критерию
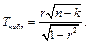
Через частные коэффициенты корреляции можно другим способом определить остаточную дисперсию. Например:
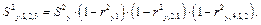
Эта формула показывает, как уменьшается «необъяснимая» часть результативного признака при последовательном введении новых факторов.
При подборе факторов, которые существенно влияют на показатель, часто используются коэффициенты частной детерминации. Коэффициент частной детерминации – это часть вариации показателя, который объясняется введением в уравнение регрессии дополнительного фактора. Другими словами: это разность между значениями коэффициентов множественной детерминации, которые получены до и после включения в модель дополнительного фактора.
Рассмотрим коэффициенты последовательной детерминации. Для простоты возьмем 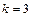 . Тогда
. Тогда
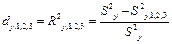
или
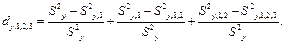
Используя коэффициенты последовательной детерминации, получим
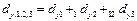
Здесь 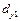 определяет долю колеблемости признака
определяет долю колеблемости признака  под влиянием фактора
под влиянием фактора 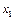 (все внутренние связи между переменными
(все внутренние связи между переменными 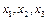 также отразятся на этом коэффициенте);
также отразятся на этом коэффициенте); 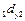 определяет дополнительную долю колеблемости
определяет дополнительную долю колеблемости  под влиянием
под влиянием 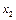 после учета влияния
после учета влияния 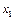 ( связь
( связь 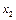 и
и 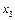 также отразятся на этом коэффициенте);
также отразятся на этом коэффициенте); 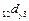 определяет дополнительную долю колеблемости
определяет дополнительную долю колеблемости  под влиянием
под влиянием 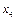 после учета влияния
после учета влияния 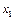 и
и 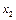 .
.
Предельный дополнительный вклад каждой переменной определяется порядком ее включения в рассмотрение.
Из формулы (3.7)
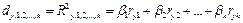
Можно получить выражение в процентах ( 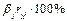 ) вклада каждого фактора
) вклада каждого фактора 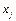 в общую объясненную колеблемость признака
в общую объясненную колеблемость признака  .
.
Дата добавления: 2016-05-11; просмотров: 1536;
