Пример решения задачи 2 контрольной работы.
Задание № 1. Для выборок величин 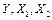 (данные приведены в таблице 3.4) найти выборочные средние
(данные приведены в таблице 3.4) найти выборочные средние 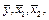 и выборочные дисперсии
и выборочные дисперсии 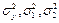 и выборочные средние квадратичные отклонения
и выборочные средние квадратичные отклонения 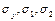 по формулам при
по формулам при 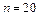 :
:
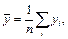
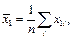
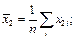
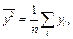
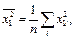
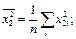
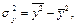
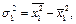
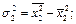
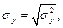
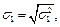
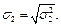
Решение. Для данных выборочных величин 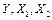 находим суммы по формулам и результаты заносим в таблицу 3.4.
находим суммы по формулам и результаты заносим в таблицу 3.4.
Таблица 3.4.
| № | 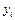
| 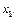
| 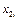
| 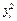
| 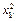
| 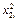
|
| 3,9 | 4.1 | 5,1 | 15,21 | 16,81 | 26,01 | |
| 3,7 | 2,2 | 13,69 | 4,84 | |||
| 3,5 | 2,7 | 5,5 | 12,25 | 7,29 | 30,25 | |
| 4,3 | 3,6 | 6,1 | 18.49 | 12,96 | 37,21 | |
| 3,8 | 3,9 | 6,9 | 14,44 | 15,21 | 47,61 | |
| 2,8 | 0,6 | 3,8 | 7,84 | 0,36 | 14,44 | |
| 2,9 | 2,1 | 5,5 | 8,41 | 4,41 | 30,25 | |
| 4,8 | 3,5 | 6,9 | 23,04 | 12,25 | 47,61 | |
| 3,8 | 4,4 | 5,5 | 14,44 | 19,36 | 30,25 | |
| 3,2 | 3,8 | 5,3 | 10,24 | 14,44 | 28,09 | |
| 4,8 | 3.7 | 6,4 | 23,04 | 13,69 | 40,96 | |
| 3,6 | 2,9 | 4,4 | 12,96 | 8,41 | 19,36 | |
| 3,6 | 3,2 | 7,1 | 12,96 | 10,24 | 50,41 | |
| 3,4 | 4,2 | 5,5 | 11,56 | 17,64 | 30,25 | |
| 3,2 | 2,7 | 5,7 | 10,24 | 7,29 | 32,49 | |
| 2,8 | 2,6 | 4,7 | 7,84 | 6,76 | 22,09 | |
| 1,9 | 1.6 | 4,3 | 3,61 | 2,56 | 18,49 | |
| 3.7 | 2,3 | 5,6 | 13,69 | 5,29 | 31,36 | |
| 3,4 | 3,1 | 6,3 | 11,56 | 9,61 | 39,69 | |
| 4.7 | 3,7 | 7.2 | 22,09 | 13,69 | 51,84 | |
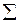
| 71,8 | 60,9 | 111,8 | 267,6 | 203,11 | 644,66 |
По полученным данным, используя формулы, находим выборочные средние:
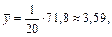
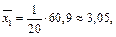
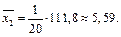
Средние квадратов:
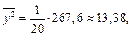
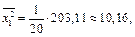
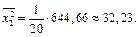
Выборочные дисперсии:
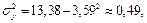
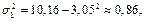
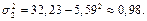
Выборочные средние квадратичные отклонения: 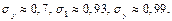
Задание №2. Используя полученные данные, найти выборочные коэффициенты корреляции: 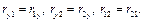
Расчетные формулы
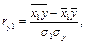
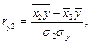
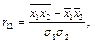
где
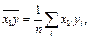
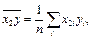
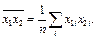
Результаты записать в виде корреляционной матрицы:
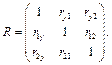
Используя критерий Стьюдента, проверить значимость коэффициентов 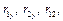 для чего вычислить
для чего вычислить 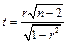 при
при 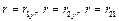 и сравнить с критическим значением
и сравнить с критическим значением 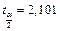 (для
(для 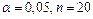 ). Коэффициент будет значимым, если
). Коэффициент будет значимым, если 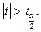
Решение: Промежуточные результаты занесем в таблицу 3.5:
Таблица 3.5
| № | 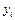
| 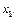
| 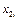
| 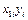
| 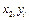
| 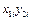
|
| 3,9 | 4,1 | 5,1 | 15,99 | 19,89 | 20,91 | |
| 3,7 | 2,2 | 8,14 | 14,8 | 8,8 | ||
| 3,5 | 2,7 | 5,5 | 9,45 | 19,25 | 14,85 | |
| 4,3 | 3,6 | 6,1 | 15,48 | 26,23 | 21,96 | |
| 3,8 | 3,9 | 6,9 | 14,82 | 26,22 | 26,91 | |
| 2,8 | 0,6 | 3,8 | 1,68 | 10,64 | 2,28 | |
| 2,9 | 2,1 | 5,5 | 6,09 | 15,95 | 11,55 | |
| 4,8 | 3,5 | 6,9 | 16,8 | 33,12 | 24,15 | |
| 3,8 | 4,4 | 5,5 | 16,72 | 20,9 | 24,2 | |
| 3,2 | 3,8 | 5,3 | 12,16 | 16,96 | 20,14 | |
| 4,8 | 3,7 | 6,4 | 17,76 | 30,72 | 23,68 | |
| 3,6 | 2,9 | 4,4 | 10,44 | 15,84 | 12,76 | |
| 3,6 | 3,2 | 7,1 | 11,52 | 25,56 | 22,72 | |
| 3,4 | 4,2 | 5,5 | 14,28 | 18,7 | 23,1 | |
| 3,2 | 2,7 | 5,7 | 8,64 | 18,24 | 15,39 | |
| 2,8 | 2,6 | 4,7 | 7,28 | 13,16 | 12,22 | |
| 1,9 | 1,6 | 4,3 | 3,04 | 8,17 | 6,88 | |
| 3,7 | 2,3 | 5,6 | 8,51 | 20,72 | 12,88 | |
| 3,4 | 3,1 | 6,3 | 10,54 | 21,42 | 19,53 | |
| 4,7 | 3,7 | 7,2 | 17,39 | 33,84 | 26,64 | |
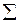
| 71,8 | 60,9 | 111,8 | 226,73 | 410,33 | 351,55 |
Находим
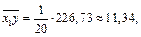
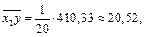
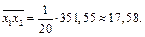
Находим выборочные коэффициенты корреляции:
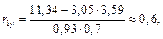
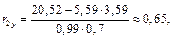
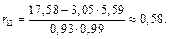
Результаты запишем в виде корреляционной матрицы:
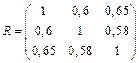
Используя критерий Стьюдента, проверим значимость коэффициентов 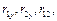 для чего вычислим:
для чего вычислим: 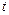 для
для 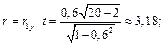
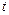 для
для 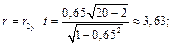
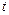 для
для 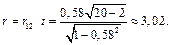
Так как полученные значения больше критического значения 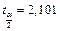 , то коэффициенты
, то коэффициенты 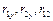 будут значимыми.
будут значимыми.
Задание №3. Используя найденные коэффициенты корреляции, получить уравнения линейной регрессии  на
на 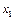 и
и  на
на 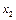 . Расчетные формулы:
. Расчетные формулы:
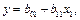
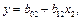
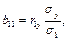
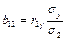
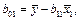
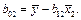
Найти коэффициенты детерминации 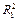 и
и 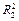 по формулам
по формулам
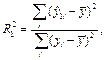
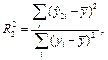 где
где
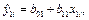
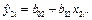
Решение: Найдем коэффициенты 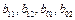 :
:
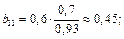
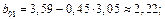
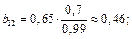
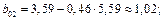
Промежуточные данные занесены в таблицу 3.6.
Таблица 3.6.
| № | 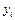
| 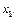
| 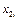
| 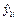
| 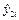
| 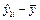
| 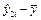
| 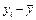
| 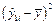
| 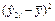
| 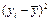
|
| 3,9 | 4,1 | 5,1 | 4,1 | 3,4 | 0,51 | -0,19 | 0,31 | 0,2601 | 0,0361 | 0,0961 | |
| 3,7 | 2,2 | 3,2 | 2,9 | -0,39 | -0,69 | 0,11 | 0,1521 | 0,4761 | 0,0121 | ||
| 3,5 | 2,7 | 5,5 | 3,4 | 3,6 | -0,19 | 0,01 | -0,09 | 0,0361 | 0,0001 | 0,0081 | |
| 4,3 | 3,6 | 6,1 | 3,8 | 3,8 | 0,21 | 0,21 | 0,71 | 0,0441 | 0,0441 | 0,5041 | |
| 3,8 | 3,9 | 6,9 | 4,2 | 0,41 | 0,61 | 0,21 | 0,1681 | 0,3721 | 0,0441 | ||
| 2,8 | 0,6 | 3,8 | 2,5 | 2,8 | -1,09 | -0,79 | -0,79 | 1,1881 | 0,6241 | 0,6241 | |
| 2,9 | 2,1 | 5,5 | 3,2 | 3,6 | -0,39 | 0,01 | -0,69 | 0,1521 | 0,0001 | 0,4761 | |
| 4,8 | 3,5 | 6,9 | 3,8 | 4,2 | 0,21 | 0,61 | 1,21 | 0,0441 | 0,3721 | 1,4641 | |
| 3,8 | 4,4 | 5,5 | 4,2 | 3,6 | 0,61 | 0,01 | 0,21 | 0,3721 | 0,0001 | 0,0441 | |
| 3,2 | 3,8 | 5,3 | 3,9 | 3,5 | 0,31 | -0,09 | -0,39 | 0,0961 | 0,0081 | 0,1521 | |
| 4,8 | 3,7 | 6,4 | 3,9 | 0,31 | 0,41 | 1,21 | 0,0961 | 0,1681 | 1,4641 | ||
| 3,6 | 2,9 | 4,4 | 3,5 | -0,09 | -0,59 | 0,01 | 0,0081 | 0,3481 | 0,0001 | ||
| 3,6 | 3,2 | 7,1 | 3,7 | 4,3 | 0,11 | 0,71 | 0,01 | 0,0121 | 0,5041 | 0,0001 | |
| 3,4 | 4,2 | 5,5 | 4,1 | 3,6 | 0,51 | 0,01 | -0,19 | 0,2601 | 0,0001 | 0,0361 | |
| 3,2 | 2,7 | 5,7 | 3,4 | 3,6 | -0,19 | 0,01 | -0,39 | 0,0361 | 0,0001 | 0,1521 | |
| 2,8 | 2,6 | 4,7 | 3,4 | 3,2 | -0,19 | -0,39 | -0,79 | 0,0361 | 0,1521 | 0,6241 | |
| 1,9 | 1,6 | 4,3 | 2,9 | -0,69 | -0,59 | -1,69 | 0,4761 | 0,3481 | 2,8561 | ||
| 3,7 | 2,3 | 5,6 | 3,3 | 3,6 | -0,29 | 0,01 | 0,11 | 0,0841 | 0,0001 | 0,0121 | |
| 3,4 | 3,1 | 6,3 | 3,6 | 3,9 | 0,01 | 0,31 | -0,19 | 0,0001 | 0,0961 | 0,0361 | |
| 4,7 | 3,7 | 7,2 | 3,9 | 4,3 | 0,31 | 0,71 | 1,11 | 0,0961 | 0,5041 | 1,2321 | |
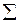
| 71,8 | 60,9 | 3,618 | 4,054 | 9,838 |
Уравнения линии регрессии имеют вид:
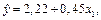
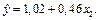
Находим коэффициенты детерминации:
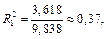
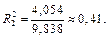
Задание №4. Найти уравнение множественной регрессии  на
на 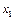 и
и 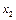 . Для этого сначала составить и решить систему уравнений
. Для этого сначала составить и решить систему уравнений
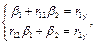
затем найти коэффициенты 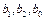 по формулам
по формулам
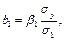
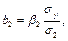
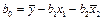
и записать уравнение регрессии 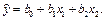
Решение. Для нашего случая система имеет вид
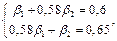
Найдем значения 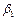 и
и 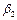 :
:
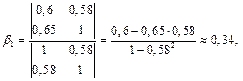
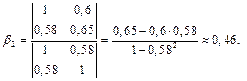
Находим коэффициенты 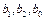 :
: 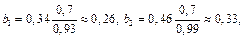
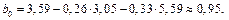
В нашем случае уравнение регрессии имеет вид 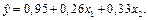
Задание №5. Найти коэффициент множественной детерминации 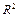
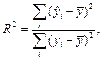
его скорректированное значение
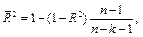
где 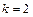 - число независимых переменных, проверить значимость
- число независимых переменных, проверить значимость 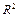 . Для этого вычислить наблюдаемое значение
. Для этого вычислить наблюдаемое значение
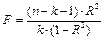
и сравнить его с критическим значением 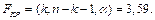 Если
Если 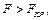 гипотеза об одновременном равенстве нулю коэффициентов
гипотеза об одновременном равенстве нулю коэффициентов 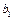 и
и 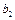 должна быть отвергнута, т.е. хотя бы один из коэффициентов
должна быть отвергнута, т.е. хотя бы один из коэффициентов 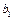 и
и 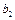 значимо отличаются от нуля.
значимо отличаются от нуля.
Решение. Для нахождения 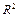 используем данные таблиц 3.4 и 3.6, промежуточные данные занесем в таблицу 3.7.
используем данные таблиц 3.4 и 3.6, промежуточные данные занесем в таблицу 3.7.
Таблица 3.7.
| № | 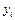
| 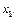
| 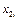
| 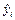
| 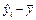
| 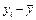
| 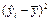
| 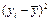
|
| 3,9 | 4,1 | 5,1 | 3,7 | 0,11 | 0.31 | 0,0121 | 0,0961 | |
| 3,7 | 2,2 | 2,8 | -0,79 | 0.11 | 0,6241 | 0,0121 | ||
| 3,5 | 2,7 | 5,5 | 3.5 | -0,09 | -0,09 | 0,0081 | 0,0081. | |
| 4,3 | 3,6 | 6.1 | 3,9 | 0,31 | 0,71 | 0,0961 | 0,5041 | |
| 3,8 | 3,9 | 6,9 | 4,2 | 0,61 | 0,21 | 0,3721 | 0,0441 | |
| 2,8 | 0,6 | 3,8 | 2,4 | -1,19 | -0,79 | 1,4161 | 0,6241 | |
| 2,9 | 2,1 | 5,5 | 3,3 | -0,29 | -0,69 | 0,0841 | 0,4761 | |
| 4,8 | 3.5 | 6,9 | 4,1 | 0,51 | 1.21 | 0,2601 | 1,4641 | |
| 3,8 | 4.4 | 5,5 | 3,9 | 0,31 | 0,21 | 0,0961 | 0,0441 | |
| 3,2 | 3,8 | 5,3 | 3,7 | 0,11 | -0,39 | 0,0121 | 0,1521 | |
| 4,8 | 3,7 | 6,4 | 0,41 | 1,21 | 0,1681 | 1,4641 | ||
| 3,6 | 2,9 | 4,4 | 3,2 | -0,39 | 0,01 | 0,1521 | 0,0001 | |
| 3,6 | 3.2 | 7,1 | 4,1 | 0,51 | 0,01 | 0,2601 | 0,0001 | |
| 3,4 | 4,2 | 5,5 | 3,9 | 0.31 | -0,19 | 0,0961 | 0,0361 | |
| 3.2 | 2,7 | 5,7 | 3,5 | -0,09 | -0,39 | 0,0081 | 0,1521 | |
| 2,8 | 2.6 | 4,7 | 3,2 | -0,39 | -0,79 | 0,1521 | 0,6241 | |
| 1,9 | 1,6 | 4,3 | 2.8 | -0,79 | -1,69 | 0.6241 | 2,8561 | |
| 3,7 | 2,3 | 5,6 | 3,4 | -0,19 | 0,11 | 0,0361 | 0,0121 | |
| 3,4 | 3,1 | 6,3 | 3,8 | 0,21 | -0,19 | 0,0441 | 0,0361 | |
| 4,7 | 3,7 | 7,2 | 4,3 | 0,71 | 1,11 | 0,5041 | 1,2321 | |
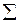
| 5,026 | 9,838 |
Находим коэффициент множественной детерминации
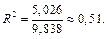
Его скорректированное значение
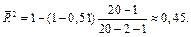
Проверим значимость 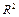 . Для этого вычислим наблюдаемое значение
. Для этого вычислим наблюдаемое значение
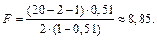
Так как выполняется условие 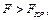 т.е.
т.е. 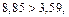 то хотя бы один из коэффициентов
то хотя бы один из коэффициентов 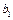 и
и  значимо отличаются от нуля.
значимо отличаются от нуля.
Задание 6. Найти коэффициенты частной корреляции 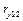 и
и 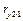 между
между 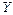 и одним из параметров
и одним из параметров 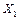 ,
, 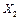 при исключении влияния другого. Расчетные формулы:
при исключении влияния другого. Расчетные формулы:
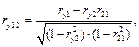
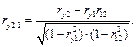
Проверить значимость коэффициентов по критерию Стьюдента. Сделать выводы.
Решение. Находим коэффициенты частной корреляции 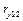 и
и 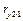 используя данные из решения задачи №2.
используя данные из решения задачи №2.
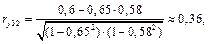
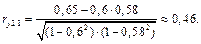
Используя критерий Стьюдента, проверим значимость коэффициентов 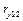 ,
, 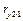 для чего вычислим:
для чего вычислим:
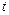 для
для 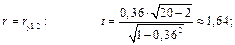
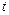 для
для 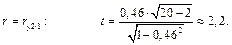
Так как в первом случае полученное значение меньше критического значения 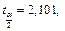 то коэффициент
то коэффициент 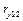 не будет значимым, а во втором случае полученное значение боль критического значения
не будет значимым, а во втором случае полученное значение боль критического значения 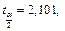 значит коэффициент
значит коэффициент 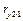 будет значимым.
будет значимым.
Задание №7. Используя критерий Дарбина - Уотсона, проверить данные на наличие автокорреляции. Для этого вычислить величины остатков 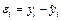 и величину
и величину 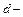 статистики
статистики
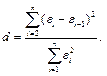
Сравнить полученные данные со значениями 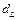 и
и 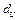 , найденными по таблице (для
, найденными по таблице (для 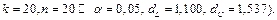 Если
Если 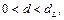 имеется положительная корреляция, если
имеется положительная корреляция, если 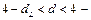 отрицательная. При
отрицательная. При 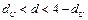 автокорреляция отсутствует. В остальных случаях нельзя сделать вывод ни о наличии автокорреляции, ни о ее отсутствии.
автокорреляция отсутствует. В остальных случаях нельзя сделать вывод ни о наличии автокорреляции, ни о ее отсутствии.
Решение. Используя исходные данные и данные задачи №5 составим таблицу 3.8, в которую занесем данные 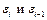 .
.
Вычислим величину 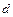 -статистики.
-статистики.
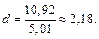
Так как выполняется условие 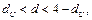 т.е.
т.е. 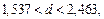 делаем вывод, что автокорреляция отсутствует.
делаем вывод, что автокорреляция отсутствует.
Таблица 3.8.
| № | 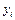
| 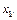
| 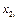
| 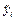
| 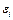
| 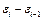
| 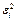
| 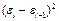
| |||
| 3,9 | 4,1 | 5,1 | 3,7 | 0,2 | - | 0,04 | - | ||||
| 3,7 | 2,2 | 2,8 | 0,9 | 0,7 | 0,81 | 0,49 | |||||
| 3,5 | 2,7 | 5,5 | 3,5 | -0,9 | 0,81 | ||||||
| 4,3 | 3,6 | 6,1 | 3,9 | 0,4 | 0,4 | 0,16 | 0,16 | ||||
| 3,8 | 3,9 | 6,9 | 4,2 | -0,4 | -0,8 | 0,16 | 0,64 | ||||
| 2,8 | 0,6 | 3,8 | 2,4 | 0,4 | 0,8 | 0,16 | 0,64 | ||||
| 2,9 | 2,1 | 5,5 | 3,3 | -0,4 | -0,8 | 0,16 | 0,64 | ||||
| 4,8 | 3,5 | 6,9 | 4,1 | 0,7 | 1,1 | 0,49 | 1,21 | ||||
| 3,8 | 4,4 | 5,5 | 3,9 | -0,1 | -0,8 | 0,01 | 0,64 | ||||
| 3,2 | 3,8 | 5,3 | 3,7 | -0,5 | -0,4 | 0,25 | 0,16 | ||||
| 4,8 | 3,7 | 6,4 | 0,8 | 1,3 | 0,64 | 1,69 | |||||
| 3,6 | 2,9 | 4,4 | 3,2 | 0,4 | -0,4 | 0,16 | 0,16 | ||||
| 3,6 | 3,2 | 7,1 | 4,1 | -0,5 | -0,9 | 0,25 | 0,81 | ||||
| 3,4 | 4,2 | 5,5 | 3,9 | -0,5 | 0,25 | ||||||
| 3,2 | 2,7 | 5,7 | 3,5 | -0,3 | 0,2 | 0,09 | 0,04 | ||||
| 2,8 | 2,6 | 4,7 | 3,2 | -0,4 | -0,1 | 0,16 | 0,01 | ||||
| 1,9 | 1,6 | 4,3 | 2,8 | -0,9 | -0,5 | 0,81 | 0,25 | ||||
| 3,7 | 2,3 | 5,6 | 3,4 | 0,3 | 1,2 | 0,09 | 1,44 | ||||
| 3,4 | 3,1 | 6,3 | 3,8 | -0,4 | -0,7 | 0,16 | 0,49 | ||||
| 4,7 | 3,7 | 7,2 | 4,3 | 0,4 | 0,8 | 0,16 | 0,64 | ||||
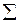
| 5,01 | 10,92 | |||||||||
Контрольная работа по курсу «Эконометрия»
Дата добавления: 2016-05-11; просмотров: 871;
