Бесконечно малая функция (б.м.ф.) и ее свойства.
Определение.Функция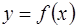 
называется бесконечно малой при 
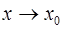, если
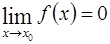. (1)
По определению предела функции равенство (1) означает: для любого числа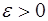 
найдется число 
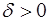такое, что для всех 
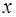, удовлетворяющих неравенству 
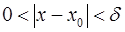, выполняется неравенство 
.
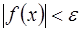Аналогично определяется б.м.ф. при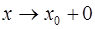 
, 
, 
, 
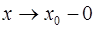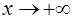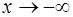: во всех этих случаях 
.
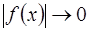Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами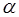 
, 
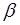и т. д.
Примерами б.м.ф. служат функции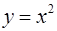 
при 
; 
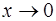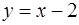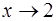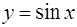при 
; 
при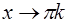 
, 
.
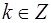Другой пример: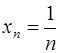 
, 
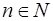, — бесконечно малая последовательность.
При решении задач пользуются теоремами о бесконечно малых, которые формулируются ниже.
Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Теорема 2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
Следствие 1.Так как всякая б.м.ф, ограничена, то из теоремы (2) вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Дата добавления: 2016-11-28; просмотров: 1573;