Сравнение бесконечно малых.
При решении задач полезно сравнить б. м. по скорости их стремления к нулю.
Пусть 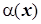 и
и 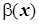 - б. м. при
- б. м. при 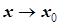
Составим их отношение 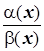 и найдем предел.
и найдем предел.
Возможны 4 случая:
1) 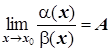 ,
, 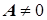 ,
, 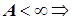
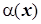 и
и 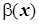 - б. м. одного порядка малости.
- б. м. одного порядка малости.
2) 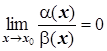 ,
, 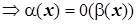 -
- 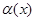 более высокого порядка малости.
более высокого порядка малости.
3) 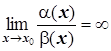 ,
, 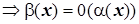 -
- 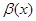 более высокого порядка малости.
более высокого порядка малости.
4) 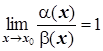 ,
, 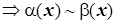 эквивалентны
эквивалентны
Теорема о замене на эквивалентную величину в пределе.
Теорема. Пусть 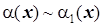 ,
, 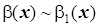 при
при 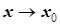 и
и 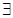
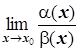 . Тогда
. Тогда 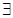
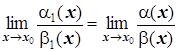 .
.
Таблица эквивалентностей
Известно, что при 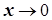
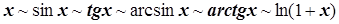 .
.
Замечание. Сравнение б. б. аналогично сравнению б. м.
Рассмотрим некоторые примеры вычисления пределов функций..
Пример. Вычислить 1) 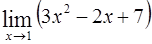 .
.
Решение:
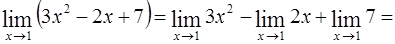
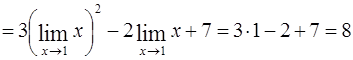 .
.
Пример. Вычислить 2) 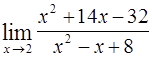 .
.
Решение: Здесь применить теорему о пределе дроби нельзя, т. к. предел знаменателя, при 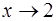 , равен
, равен  . Кроме того, предел числителя равен
. Кроме того, предел числителя равен  . В таких случаях говорят, что имеем неопределенность вида
. В таких случаях говорят, что имеем неопределенность вида 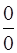 . Для ее раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на
. Для ее раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на 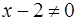 (
( 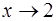 , но
, но 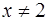 ) :
) :
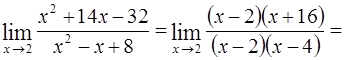
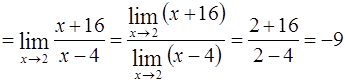 .
.
3) 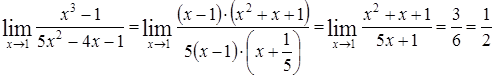 .
.
4) 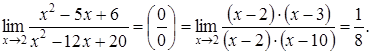
Вычисление пределов иррациональных функций.
Пример.
5)
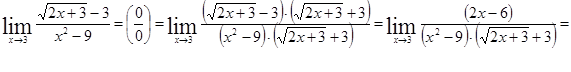
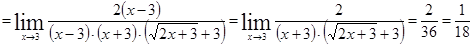 .
.
6) 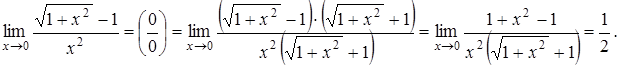
Вычисление пределов отношения бесконечно больших функций, т.е. при неопределенности вида 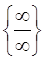
Пример.7)Вычислить предел функции 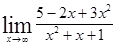 .
.
Решение. Сократим числитель и знаменатель дроби на самую большую степень x, т.е. на x2 (дробь при этом не изменится):

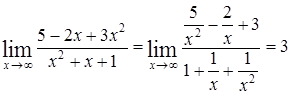 .
.
Дата добавления: 2016-11-28; просмотров: 885;
