Бесконечно-малые и бесконечно-большие величины.
Определение. Функция 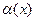 называется бесконечно-малой в точке
называется бесконечно-малой в точке 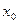 , если
, если 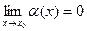 .
.
Функция 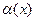 называется бесконечно-большой в точке
называется бесконечно-большой в точке 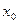 , если
, если 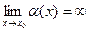 .
.
Это понятие не применимо к функции «вообще», без указания точки. Не бывает просто «бесконечно-малой функции», бывает только «бесконечно-малая функция в точке». Это свойство поведения функции в конкретной точке. Так, 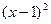 является бесконечно-малой при
является бесконечно-малой при 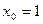 .
.
Очевидно, что если 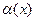 беск-малая в точке, то
беск-малая в точке, то 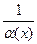 является бесконечно-большой в той же точке.
является бесконечно-большой в той же точке.
Пример. Фкнкция 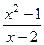 является бесконечно малой в точках
является бесконечно малой в точках 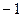 и 1 и бесконечно большой в точке 2.
и 1 и бесконечно большой в точке 2.
Бесконечно малые называются сравнимыми, если существует хотя бы один из пределов 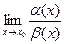 или
или 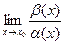 .
.
Если 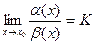 , причём
, причём 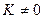 и
и 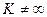 , то две функции называются бесконечно-малыми ОДНОГО ПОРЯДКА малости. Кстати, тогда
, то две функции называются бесконечно-малыми ОДНОГО ПОРЯДКА малости. Кстати, тогда 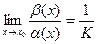 , то есть оба предела равны конечным числам, а не
, то есть оба предела равны конечным числам, а не 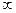 . Если было бы
. Если было бы 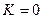 то второй предел был бы
то второй предел был бы 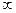 .
.
Если при этом 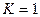 , то есть
, то есть 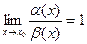 , то две бесконечно малые называются ЭКВИВАЛЕНТНЫМИЭто частный случай той ситуации, когда они одного порядка.
, то две бесконечно малые называются ЭКВИВАЛЕНТНЫМИЭто частный случай той ситуации, когда они одного порядка.
Пример. 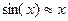 .
.
Если 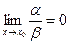 то
то 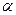 называется бесконечно-малой более высокого порядка, чем
называется бесконечно-малой более высокого порядка, чем 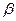 .
.
Пример. 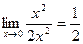 . Функции
. Функции 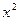 и
и 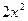 одного порядка в точке 0.
одного порядка в точке 0.
Пример. 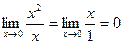 , а также
, а также 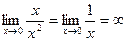 ,
,
то есть 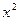 более высокого порядка, чем
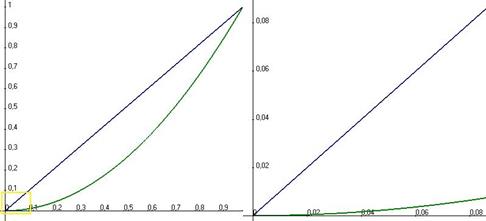
более высокого порядка, чем 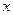 . И хотя они обе стремятся к 0, но скорость этого процесса кардинально отличается. Если рассмотреть их графики при большом увеличении около начала координат, то парабола почти неотличима от оси 0х.
. И хотя они обе стремятся к 0, но скорость этого процесса кардинально отличается. Если рассмотреть их графики при большом увеличении около начала координат, то парабола почти неотличима от оси 0х.
Третья степень - ещё более высокого порядка, она будет проходить ниже, чем парабола. Как мы видим, хоть и все они стремятся к 0, но эти нули как бы совершенно разной силы.
Дата добавления: 2016-12-26; просмотров: 762;
