МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ II ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений

Если случайная величина Х характеризуется конечным рядом распределения:

то математическое ожидание М(X) определяется по формуле

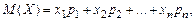или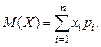

Так как 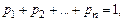то

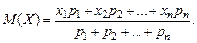
Таким образом, М(X) является взвешенной средней арифметической случайной величины х₁, х₂,… х_п при весах р₁, р₂,… р_п.

Если 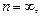то 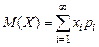(при условии, что ряд абсолютно сходится).

Понятие математического ожидания распространяется и на непрерывную случайную величину. Пусть 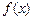– плотность вероятности случайной величины Х. Тогда математическое ожидание непрерывной случайной величины Х определяется равенством

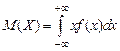
(при условии, что интеграл абсолютно сходится).

Геометрически математическое ожидание как непрерывной, так и дискретной случайной величины равно абсциссе центра тяжести площади, ограниченной кривой (или полигоном) распределения и осью абсцисс. Поэтому при симметрии кривой (или полигона) распределения относительно некоторой прямой, параллельной оси ординат, математическое ожидание совпадает с абсциссой точки пересечения этой оси симметрии с осью абсцисс.

Точка оси Ох, имеющая абсциссу, равную математическому ожиданию случайной величины, часто называется центром распределения этой случайной величины.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

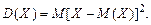
Если ввести обозначение М(Х) = т, то формулы для вычисления дисперсии дискретной случайной величины Х запишутся в виде

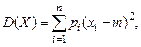
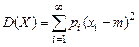(при ),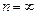

а для непрерывной случайной величины Х – в виде

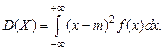
Для дисперсии случайной величины справедлива формула

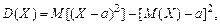или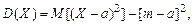

где а – произвольное число. Этой формулой часто пользуются для вычисления дисперсии случайной величины, так как вычисление по этой формуле обычно проще.

Средним квадратичным отклонением случайной величины Х называется величина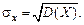

Среднее квадратичное отношение есть мера рассеяния значений случайной величины около её математического ожидания.