СЛУЧАЙНОЕ СОБЫТИЕ, ЕГО ЧАСТОТА И ВЕРОЯТНОСТЬ. ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
Основными понятиями в теории вероятностей являются понятия события и вероятности события.
Под событием понимается такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может произойти или не произойти.
События будем обозначать буквами А, В, С, .... Если событие неизбежно произойдет при каждой реализации комплекса условии, то оно называется достоверным; если же оно не может произойти – невозможным.
Если событие А при реализации комплекса условий может произойти, а может и не произойти, то оно называется случайным.
Событие, состоящее в наступлении хотя бы одного из событий А и В, будем называть суммой (объединением) событии А и В и обозначать А+В или АÈВ.
Событие, состоящее в наступлении обоих событий А и В, будем называть произведением (совмещением) событии А и В и обозначать АВ или АÇВ.
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пусть, например, нас интересует появление определенного числа очков на грани при одном бросании игральной кости: i = 1,2,3,4,5,6. Выпадение конкретного числа очков назовем элементарным событием (исходом), которое обозначим wi. Таким образом, для каждого связанного с этим опытом события А можно выделить совокупность тех элементарных исходов w, наступление которых влечет за собой наступление события А.
Пусть событие А состоит в появлении нечётного числа очков на грани. Этому событию благоприятствуют элементарные события w1, w3, w5, т.е. некоторое подмножество множества всех элементарных исходов w1, w2, w3, w4, w5, w6.
Совокупность элементарных событий обозначается W и называется пространством элементарных событий.
Элементарные события взаимно исключают друг друга и в результате данного опыта обязательно произойдет одно из них. Пространство элементарных событии образует так называемую полную группу попарно несовместных событий, так как появление хотя бы одного из событии полной группы есть достоверное событие.
Два несовместных события, образующих полную группу, называются противоположными. Для противоположных событий одновременно выполняются два условия: 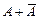 – достоверное событие и
– достоверное событие и 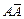 – невозможное событие.
– невозможное событие.
Для количественной оценки возможности появления случайногособытия Авводится понятие вероятности.
Вероятностью события А называют отношение числа m исходов, благоприятствующих этому событию, к числу n всех равновозможных несовместных элементарных исходов, образующих полную группу:
P(А)=m/n
(классическое определение вероятности).
В рассмотренном примере вероятность выпадения грани с нечётнымчисломочков составляет Р(А) = 3/6 = 1/2.
Приведём аксиоматическое определение вероятности, предложенное А.Н. Колмогоровым.
1°. Каждому случайному событию А из поля событий ставится в соответствиенеотрицательноечисло Р(А), называемоевероятностью.
2°. Р(W) = 1.
3°. Аксиома сложения. Если события А1, А2, …, Аk, попарно несовместны, то Р(А1 + А2 +…+ Аk) = Р(А1) + Р(А2) +…+ Р(Аk).
Отсюда следует, что:
1) вероятность невозможного события равна нулю;
2) для любого события А 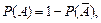 где
где 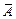 – противоположное событие;
– противоположное событие;
3) каково бы ни было случайное событие А, 0 £ Р(А) £1.
Используя аксиомы, свойства вероятностей выводят в качестве теорем.
К числу основных понятий теории вероятностей также относится частота события, под которой понимают отношение числа испытании, в которых это событие произошло, к общему числу фактически произведенных испытаний. Частоту события называют статистической вероятностью. Для вычисления частоты события необходимо произвести в действительности испытания (опыт), что не требуется для определения вероятности.
Массовые случайные события обладают свойством устойчивости частоты:наблюдаемые в различных сериях однородных испытаний (с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах и стремятся (по вероятности) к некоторому постоянному числу. При этих условиях частоту можно принять за приближенное значение вероятности.
При классическом определении вероятности не всегда можно определить числа т и п для вычисления вероятностей событий, и поэтому непосредственно пользоваться формулой Р(А)== т/п не удаётся. В таких случаях вводят понятие геометрической вероятности, т. е. вероятности попадания точки в область (отрезок, часть плоскости, часть тела и т. д.).
Пусть, например, па плоскости имеется некоторая область G и в ней содержится другая область g. Требуется найти вероятность того, что точка, взятая наудачу в области G, попадет в область g. При этом выражению «точка, взятая наудачу в области G» придается следующий смысл: эта точка может попасть в любую точку области G. Вероятность попадания точки в какую-либо часть области g пропорциональна мере (mes) этой части (длине, площади, объему и т.д.) и не зависит от ее расположения и формы:
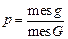
(геометрическое определение вероятности).
2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. УСЛОВНАЯ ВЕРОЯТНОСТЬ
Теорема сложения вероятностей. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Р(А+В) = Р(А) + Р(В).
Эта теорема обобщается на случай произвольного числа попарно несовместных событий:
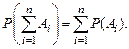
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А/В).
Условие независимости события А от события В можно записать в виде Р(А/В) =Р(А), а условие зависимости – в виде Р(А/В) ¹ Р(А).
Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
Р(АВ) = Р(А)×Р(В/А) или Р(АВ) = Р(В)×Р(А/В).
Если событие А не зависит от события В, то и событие В не зависит от события А; тогда
Р(АВ)=Р(А)×Р(В).
Условная вероятность события Аk определённая в предположении, что осуществились события А1, А2, …, Аk–1, обозначается Р(Аk/А1А2…Аk–1).
Вероятность произведения нескольких, событий равна произведению вероятностей этих событий, причем вероятность каждого следующею по порядку события вычисляется при условии, что все предыдущие имели место:
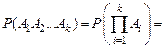
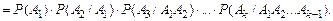
В случае независимых событий справедлива формула
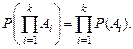
Дата добавления: 2016-05-11; просмотров: 1556;
