ПОКАЗАТЕЛЬНОЕ (ЭКСПОНЕНЦИАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ. ФУНКЦИЯ НАДЕЖНОСТИ.
Аналогом закона Пуассона для непрерывных случайных величин служит показательный (экспоненциальный) закон, функция плотности распределения которого имеет вид
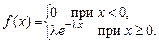
где l > 0 – постоянный параметр.
Функция распределения (интегральная функция) показательного закона
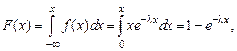
т. е.
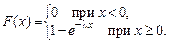
Вероятность попадания случайной величины Х в интервал (a, b) составляет
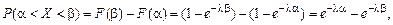
т. е.
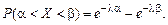
Определим числовые характеристики показательного закона распределения:
математическое ожидание
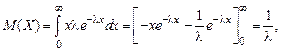
дисперсия
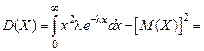
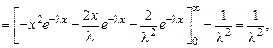
среднее квадратичное отклонение
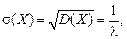 т.е.
т.е. 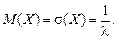
Если Т – непрерывная случайная величина, выражающая продолжительность времени безотказной работы какого-либо элемента, а l – интенсивность отказов (среднее число отказов в единицу времени), то продолжительность времени t безотказной работы этого элемента можно считать случайной величиной, распределённой по показательному закону с функцией распределения 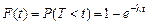 (l > 0), которая определяет вероятность отказа элемента за время t.
(l > 0), которая определяет вероятность отказа элемента за время t.
Функция надежности R(t) определяет вероятность безотказной работы элемента за время t: 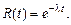
Дата добавления: 2016-05-11; просмотров: 835;
