ФОРМУЛА БЕРНУЛЛИ. НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО НАСТУПЛЕНИЙ СОБЫТИЯ.

Если производится п независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р, то вероятность того что событие А появится в этих п испытаниях т раз, выражается формулой Бернулли

где q = 1 – р. Таким образом,

…,

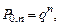
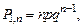
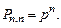
Число m₀ называется наивероятнейшим числом наступления события А в n испытаниях, если значение Р_m,п при m = т₀ не меньше остальных значений Р_т,n, т. е. 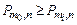при m_i ¹ т₀.

Если р ¹ 0 и р ¹ 1, то число т₀ можно определить из двойного неравенства

пр – q £ т₀ £ пр + р.

Разность граничных значений в этом двойном неравенстве равна 1. Если пр + р не является целым числом, то двойное неравенство определяет лишь одно наивероятнейшее значение т₀. Если же пр + р – целое число, то имеются два наивероятнейших значения: 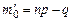и

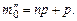
4. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БЕЙЕСА

Если известно, что событие А может произойти вместе с одним из событий Н₁, Н₂, ..., Н_п (гипотез), образующими полную группу попарно несовместных событий, то событие А можно представить как объединение событий АН₁, АН₂, ..., АН_n, т. е. А = АН₁ + АН₂ +…+ АН_n. Вероятность события А можно определить по формуле

или

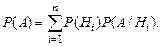
Эта формула называется формулой полной вероятности.

Условная вероятность события Н_i; в предположении, что событие А уже имеет место, определяется по формуле Бейеса:

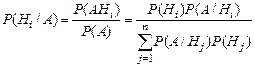(i = 1, 2, …, п).

Вероятности Р(Н_i/А), вычисленные по формуле Бейеса, часто называют вероятностями гипотез.

5. СЛУЧАЙНАЯ ВЕЛИЧИНА И ЗАКОН ЕЁ РАСПРЕДЕЛЕНИЯ.

Если каждому элементарному событию w из некоторого множества событий W можно поставить, в соответствие определенную величину Х = Х(w) говорят, что задана случайная величина. Случайную величину Х можно рассматривать как функцию события w с областью определения W.

Случайная величина может принять то или иное значение из некоторого числового множества, однако заранее неизвестно, какое именно. Случайные величины принято обозначать большими буквами Х, Y, …, а принимаемые ими значения – соответствующими строчными буквами х, у, …

Если значения, которые может принимать данная случайная величина Х, образуют дискретный (конечный или бесконечный) ряд чисел х₁, х₂,…, х_n,…, то и сама случайная величина Х называется дискретной.

Если же значения, которые может принимать данная случайная величина X заполняют конечный или бесконечный промежуток (а, b) числовой оси Ох, то случайная величина называется непрерывной.

Каждому значению случайной величины дискретного типа х_п отвечает определенная вероятность р_п; каждому промежутку (а, b) из области значений случайной величины непрерывного типа также отвечает определённая вероятность Р(а < Х < b) того, что значение, принятое случайной величиной, попадёт в этот промежуток.

Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

Закон распределения дискретной случайной величины обычно задаётся рядом распределения:

При этом 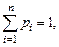где суммирование распространяется на всё (конечное или бесконечное) множество возможных значений данной случайной величины Х.Закон распределения непрерывной случайной величины удобно задавать с помощью так называемой функции плотности вероятности 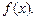Вероятность Р(а < Х < b) того, что значение, принятое случайной величиной Х, попадет в промежуток (а, b), определяется равенством

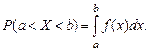
График функции 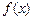называется кривой распределения. Геометрически вероятность попадания случайной величины в промежуток (а, b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х = а, х= b.

Функция плотности вероятности 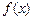обладает следующими свойствами:

1°.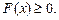

2°.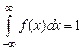

(если все значения случайной величины Х заключены в промежутке (а, b), то последнее равенство можно записать в виде ).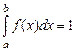

Рассмотрим теперь функцию 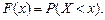Эта функция называется функцией распределения вероятности случайной величины X. Функция 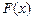существует как для дискретных, так и для непрерывных случайных величин. Если 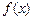– функция плотности распределения вероятности непрерывной случайной величины Х, то

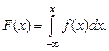
Из последнего равенства следует, что

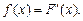
Иногда функцию 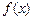называют дифференциальной функцией распределения вероятности, а функцию 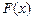– интегральной функцией распределения вероятности.

Отметим важнейшие свойства функции распределения вероятности:

1°. 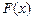– неубывающая функция.

2°.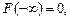

3°.

Понятие функции распределения является центральным в теории вероятностей. Используя это понятие, можно дать другое определение непрерывной случайной величины. Случайная величина называется непрерывной, если её интегральная функция распределения 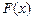непрерывна.