НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ. ФУНКЦИЯ ЛАПЛАСА.

Нормальный закон распределения характеризуется плотностью

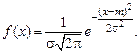
Нетрудно видеть, что функция 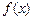удовлетворяет двум условиям, предъявляемым к плотности распределения: 1) 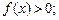2)

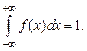
Кривая 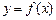симметрична относительно прямой х = т, максимальная ордината кривой (при х = т) равна 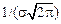и ось абсцисс является асимптотой этой кривой. Так как 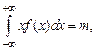то параметр т является математическим ожиданием случайной величины X. С другой стороны, 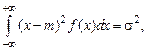откуда 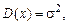т. е. (s является средним квадратичным отклонением величины X.

Введем обозначение

Функция Ф(х) называется функцией Лапласа, или интегралом вероятностей. Эту функцию называют также функцией ошибок и обозначают erf х.

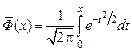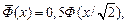Иногда используются и другие формы функции Лапласа, например, (нормированная функция Лапласа), которая связана с функцией ошибок соотношением или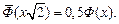

Для вычисления значений функции Лапласа пользуются специальной таблицей.

Вероятность попадания в интервал (а, b) случайной величины X, подчинённой нормальному закону, определяется через значения функции Лапласа по формуле

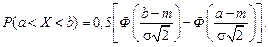
Отметим следующие свойства функции Лапласа.

1°. Ф(0) = 0, так как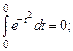

2°. 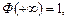поскольку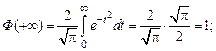

3°. Ф(х) – нечётная функция.

Справедлива также формула

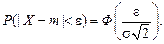
С помощью этой формулы можно находить вероятность попадания случайной величины, подчинённой нормальному закону, в интервал, симметричный относительно точки т.