ТЕОРЕМА МУАВРА – ЛАПЛАСА.
Если производится п испытаний, в каждом из которых вероятность появления события А равна р, то частота т/п появлений события является случайной величиной, распределенной по биномиальному закону, математическое ожидание и дисперсия которой равны соответственно р и 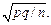 Случайная величина
Случайная величина 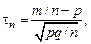 математическое ожидание которой равно нулю, а дисперсия – единице, носит название нормированной частоты случайного события (её распределение – также биномиальное).
математическое ожидание которой равно нулю, а дисперсия – единице, носит название нормированной частоты случайного события (её распределение – также биномиальное).
Теорема Муавра-Лапласа устанавливает, что при неограниченном возрастании числа п испытаний биномиальный закон распределения нормированной частоты в пределе превращается в нормальный с тем же математическим ожиданием (равным 0) и дисперсией (равной 1). В силу этого при больших значениях п для вероятностей неравенств, которым должна удовлетворять частота (или число наступлений) случайного события, можно использовать приближенную оценку с помощью интеграла вероятностей (функции Лапласа), а именно, справедливы следующие приближённые формулы:
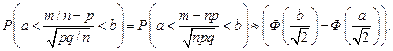
Дата добавления: 2016-05-11; просмотров: 666;
