ІІІ.5. Формула Гріна і теорема про нормальну похідну гармонічної функції.
Доведення формули Гріна базується на формулі Остроградського.
 Нехай функції
Нехай функції 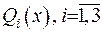 задано у області
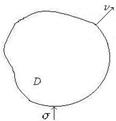
задано у області 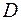 , яка обмежена кусково-гладкою поверхнею
, яка обмежена кусково-гладкою поверхнею 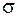 , а
, а 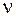 нормаль у будь-який точці цієї поверхні. Тоді формула Остроградського записується у вигляді:
нормаль у будь-який точці цієї поверхні. Тоді формула Остроградського записується у вигляді:
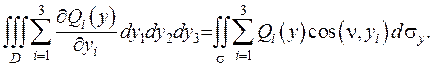 (ІІІ.13)
(ІІІ.13)
Формула (3.13) є справедливою, якщо функції 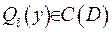 , а також
, а також 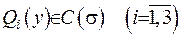 . Візьмемо за ці функції таки:
. Візьмемо за ці функції таки: 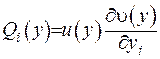 , де
, де 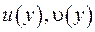 є також двічі діференціюємими -
є також двічі діференціюємими - 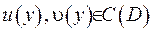 . Підрахуємо похідні функцій:
. Підрахуємо похідні функцій:
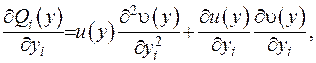
після чого проведемо підсумовування:
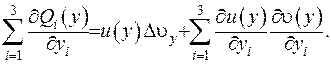 (ІІІ.14)
(ІІІ.14)
Підставимо отриману суму (ІІІ.14) у ліву частину формули Остроградського (ІІІ.3):
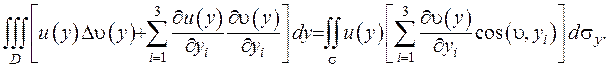
(ІІІ.15)
Можна помітити, що 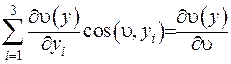 . Якщо тепер для функції
. Якщо тепер для функції 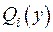 взяти зображення
взяти зображення 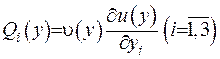 та провести аналогічні міркування, то отримаємо
та провести аналогічні міркування, то отримаємо
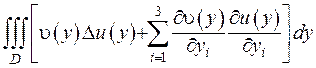
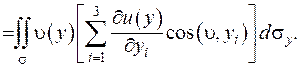
( ІІІ.16)
Від формули (ІІІ.15) віднімемо формулу (ІІІ.16):
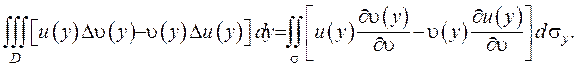
(ІІІ.17)
Помітимо, що для того, щоб формула Гріна (ІІІ.17) була справедливою, необхідно виконання наступних умов:
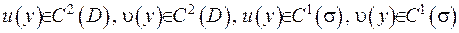 .
.
Слідство. Якщо функція є гармонічною в деякий області, то інтеграл по замкненій області, що цілком лежить в області гармонічності, дорівнює нулеві.
Доведення. Припустимо, що у формулі (ІІІ.18) функція 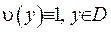 . Нехай
. Нехай 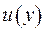 - функція, яка є гармонічною в області
- функція, яка є гармонічною в області 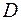 , отже,
, отже, 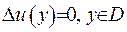 . Для функції
. Для функції 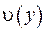 маємо
маємо 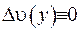 , а також
, а також 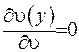 (бо нормальна похідна зображує собою комбінацію основних частинних похідних, які дорівнюють нулеві). Виходячи з формули Гріна, отримаємо
(бо нормальна похідна зображує собою комбінацію основних частинних похідних, які дорівнюють нулеві). Виходячи з формули Гріна, отримаємо
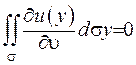 . (ІІІ.18)
. (ІІІ.18)
 ІІІ.6. Інтегральне зображення гармонічної функції.
ІІІ.6. Інтегральне зображення гармонічної функції.
Нехай 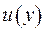 - функція, гармонічна у області
- функція, гармонічна у області 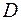 , що обмежена поверхнею
, що обмежена поверхнею 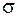 , тобто
, тобто 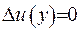 , для будь-якої точки
, для будь-якої точки 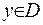 . Нехай
. Нехай 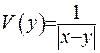 - фундаментальний розв’язок рівняння Лапласа, тобто,
- фундаментальний розв’язок рівняння Лапласа, тобто, 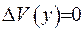 , якщо
, якщо 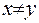 . У випадку, коли точка
. У випадку, коли точка 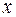 лежить у області
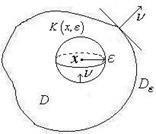
лежить у області 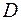 , то з метою використання формули Гріна потрібно виключити цю точку з області
, то з метою використання формули Гріна потрібно виключити цю точку з області 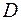 , обмежуючи ії сферою радіуса
, обмежуючи ії сферою радіуса 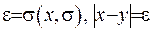 . Введемо позначення:
. Введемо позначення: 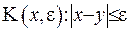 (це є вся область усередині сфери та на її поверхні),
(це є вся область усередині сфери та на її поверхні), 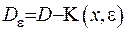 . У області
. У області 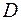 використання формули Гріна є справедливим. Будемо враховувати, що поверхня області
використання формули Гріна є справедливим. Будемо враховувати, що поверхня області 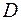 складається з двох частин
складається з двох частин 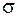 та
та 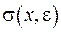 . Тоді формула Гріна (ІІІ.17) набуває вигляду:
. Тоді формула Гріна (ІІІ.17) набуває вигляду:
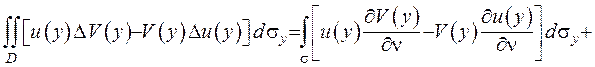
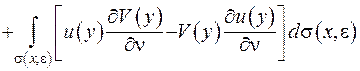 . (ІІІ.19)
. (ІІІ.19)
За умовою маємо, що 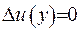 ; оскільки сфера, що містить точку
; оскільки сфера, що містить точку 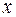 , виключена з розгляду, то
, виключена з розгляду, то 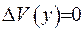 . Розглянемо докладніше другий доданок правої частини формули (ІІІ.19), який запишемо у формі
. Розглянемо докладніше другий доданок правої частини формули (ІІІ.19), який запишемо у формі
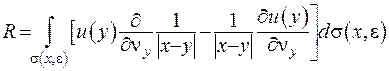 (ІІІ.20)
(ІІІ.20)
Введемо сферичну систему координат 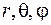 з центром у точці
з центром у точці 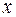 . Напрямок збільшення змінної
. Напрямок збільшення змінної 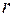 (у цієї системі координат це є радіус сфери) протилежен напрямку нормалі. Тоді
(у цієї системі координат це є радіус сфери) протилежен напрямку нормалі. Тоді
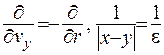 ,
,
та отже,
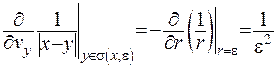 .
.
Тут маємо підкреслити, що похідна підраховується у точках сфери 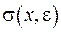 .
.
У формулі (ІІІ.20) застосуємо теорему про середнє
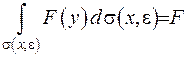
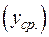
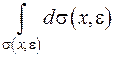 (ІІІ.21)
(ІІІ.21)
та отримаємо наступне співвідношення:
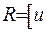
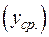
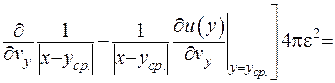
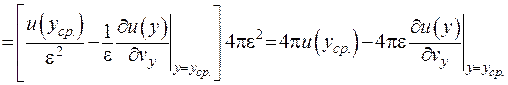 , (ІІІ.22)
, (ІІІ.22)
де 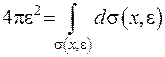 .
.
Для того, щоб перейти до розгляду всієї області 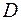 , зробимо у формулі (ІІІ.21) перехід до межі, прямуючи
, зробимо у формулі (ІІІ.21) перехід до межі, прямуючи 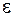 до нуля:
до нуля:
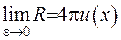 .
.
(Тут враховано, що, оскільки 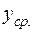 - це є довільна точка на сфері
- це є довільна точка на сфері 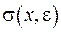 , при
, при 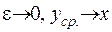 ).
).
Тоді формула Гріна буде записуватися у вигляді
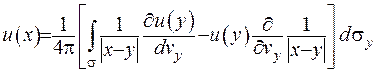 (ІІІ.23)
(ІІІ.23)
У випадку, коли 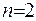 , співвідношення (ІІІ.23) набуває форму:
, співвідношення (ІІІ.23) набуває форму:
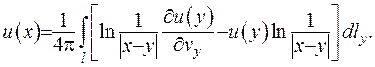 (ІІІ.24)
(ІІІ.24)
Дата добавления: 2016-05-05; просмотров: 1207;
