Асимптотична формула Пуассона
Наведених вище приклади показують, що обчислювати ймовірності 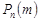 при великих n за формулою (8.2) важко, особливо, коли ймовірність
при великих n за формулою (8.2) важко, особливо, коли ймовірність 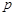 мала. Імовірність того, що рідкісна подія А (значення
мала. Імовірність того, що рідкісна подія А (значення 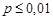 ) відбувається точно m разів при великої кількості дослідів
) відбувається точно m разів при великої кількості дослідів 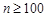 , обчислюється наближено за асимптотичною формулою Пуассона:
, обчислюється наближено за асимптотичною формулою Пуассона:
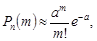 де
де 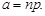 (8.3)
(8.3)
Доведемо формулу (8.3).
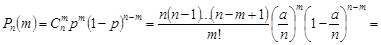
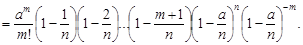
У останній рівності перейдемо до границі, коли 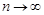 . Враховуючи, що
. Враховуючи, що 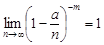 , а
, а 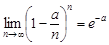 , маємо
, маємо
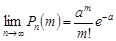 .
.
Звідси випливає асимптотична формула Пуассона.
Зауваження. На практиці формулу (8.3) застосовують, якщо добуток 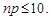
Приклад 8.4. Словник має 1500 сторінок. Імовірність друкарської помилки на одній сторінці дорівнює 0,001. Знайти ймовірність того, що в словнику: 1) буде рівно 3 помилки; 2) не буде жодної помилки; 3) буде хоча б одна помилка.
Розв’язання. 1) За умовою задачі ймовірність р = 0,001 – мала, а добуток пр =1,5 <10. Тоді за асимптотичною формулою Пуассона знаходимо
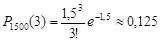 .
.
2) Імовірність того, що в словнику не буде жодної помилки, тобто m = 0, знаходимо за тією ж формулою
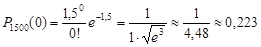 .
.
3) Подія А – у словнику буде хоча б одна помилка, є протилежною до події – у словнику немає жодної помилки. Тому
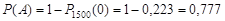 .
.
Приклад 8.5. На факультеті 1825 студентів. Яка ймовірність того, що 1 вересня буде днем народження одночасно чотирьох студентів факультету?
Розв’язання. Ймовірність того, що студент має день народження 1 вересня дорівнює 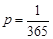 . Кількість студентів
. Кількість студентів 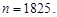 Добуток пр =
Добуток пр = 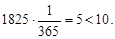 Отже, за асимптотичною формулою Пуассона (8.3) маємо
Отже, за асимптотичною формулою Пуассона (8.3) маємо
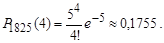
| <== предыдущая лекция | | | следующая лекция ==> |
| Грамматические тропы (аллеотеты). | | | МЕЖДУНАРОДНЫЕ ФИНАНСОВЫЕ ПОТОКИ И МИРОВЫЕ ФИНАНСОВЫЕ ЦЕНТРЫ |
Дата добавления: 2016-11-02; просмотров: 1346;
