Вторая интерполяционная формула Ньютона.
Первая интерполяционная формула Ньютона практически неудобна для интерполирования значений вблизи конца таблицы. В этом случае обычно применяется вторая интерполяционная формула Ньютона.
Pn(x)=yn+q 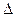 yn-1+
yn-1+ 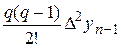 +
+ 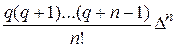 y0,
y0,
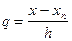
Пример: y= sin x x 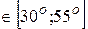 , h=5
, h=5
Горизонтальная таблица разностей.
| x | y |  y y
|  2y 2y
|  3y 3y
|  4y 4y
|  5y 5y
|
| 0.5000 | 0.0736 | -0.0044 | -0.0005 | 0.0002 | ||
| 0.5736 | 0.0692 | -0.0049 | -0.0005 | 0.0002 | ||
| 0.6428 | 0.0643 | -0.0054 | -0.0003 | |||
| 0.7071 | 0.0589 | -0.0057 | ||||
| 0.7660 | 0.0532 | |||||
| 0.8192 |
Пример: Отыщем sin(51 o), xn=51, x=50o, q=0.2
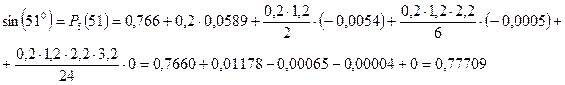
Как первая, так и вторая формула Ньютона может быть использована для экстраполирования функции, т.е. для нахождения значений функции y для значений аргументов x, лежащих вне пределов таблицы.
Если x<x0, то лучше применять первую интерполяционную функцию Ньютона.
Если x>x0, то лучше применять вторую интерполяционную функцию Ньютона.
Т.е., 1ИФН используется для интерполирования вперёд и экстраполирования назад.
2 ИФН используется для интерполирования назад и экстраполирования вперёд.
Как видно из формул 1 и 2 , при интерполяции используется разности: в 1ИФН 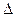 ny0 , во 2ИФН
ny0 , во 2ИФН 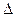 kyk+_ .
kyk+_ .
Но существуют формулы, называемые формулы с центральными разностями, к ним относятся:
- ИФ Гаусса
- ИФ Стерлинга
- ИФ Бесселя,
которые используют разности, расположенные в горизонтальной строке диагональной таблицы, соответствует начальным значениям xk, yk или в строках близлежащих.
Но все эти формулы работают только для постоянного шага.
Необходимо отметить следующее:
при построении интерполяционных формул Ньютона в качестве начального значения 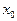 выбирается первый или последний узел интерполирования; для центральных формул начальный узел является средним.
выбирается первый или последний узел интерполирования; для центральных формул начальный узел является средним.
При 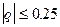 применяют формулу Стирлинга, а при
применяют формулу Стирлинга, а при 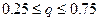 - Бесселя.
- Бесселя.
1ИФН и 2ИФН применяют тогда, когда интерполирование производится в начале или в конце таблицы и нужных центральных разностей не хватает.
Общая характеристика интерполяционных
Дата добавления: 2016-09-20; просмотров: 982;
