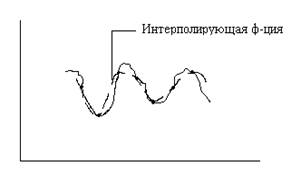
Интерполяция функций.
Первый этап работы любого вычисления - числа, приближения, погрешность.
Второй этап работы - функция, вычисления функции, её приближения. В краце о интерполяции. Интерполяция в простейшем случае заключается в следующем:
|
Постановка задачи.
На отрезке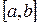 
заданы n значений аргумента x и соответствующие им значения функции f(x0)=y0; f(x1)=y1; …; f(xn)=yn.
Требуется построить функцию F(x), которая бы принимала в точках x те же значения, что и f(x):
F (x0)=y0; F (x1)=y1… F (xn)=yn
Для чего?
Для того, чтобы:
1. Задача интерполяции. Суметь по полученной функции вычислить значения F(z), где z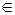 
,
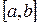z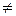 
xi при i=0,n
2. Задача экстраполяции. Суметь по полученной функции вычислить F(z), где z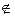 
.
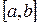Все существующие интерполяционные формулы содержат в себе конечные разности различных порядков.
Введём понятие конечных разностей.
Дата добавления: 2016-09-20; просмотров: 521;