Конечные разности различных порядков.

Пусть: y =f(x) - заданная функция

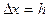- фиксированная величина приращения аргумента

Тогда 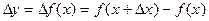- называется первой конечной разностью функции y, или конечной разностью первого порядка.

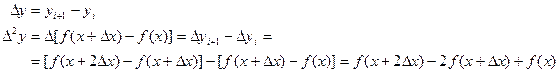
Вторая конечная разность, или конечная разность второго порядка.

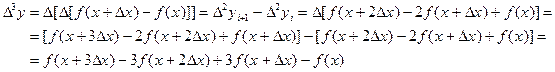
Третья конечная разность, или конечная разность третьего порядка.

Т.о., в общем виде:

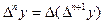
Конечная разность n-го порядка.

Пример: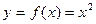

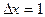
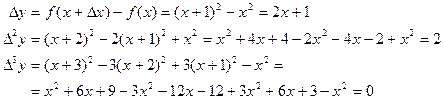
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной и диагональной таблиц разностей

x	y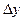
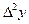
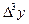
x0	y0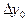
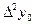
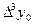
x1	y1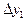
...	...	...	...	...

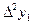
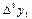
Диагональная таблица разностей.

x	y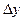
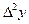
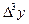
X0	Y0
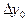
X1	Y1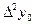
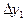
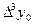
X2	Y2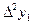
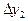
X3	Y3

Пример: горизонтальная таблица функции y = f(x) = x² при

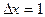, x₀ = 0 начальное значение, x₆=5 конечное значение

x	y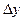

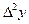
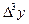
Диагональная таблица

x	y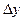

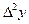
При составлении таблиц возможные ошибки вычисляются и диагональная таблица наглядно показывает нам, как отразится ошибка 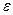в значении y_n.

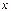
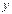
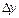
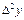
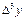
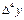
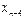
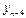
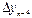
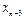
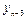
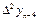
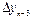
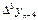
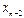
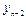
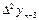
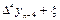
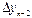
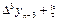
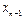
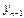
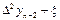
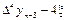
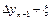
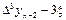
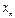
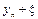
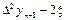
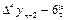
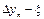
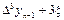
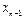
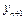
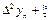
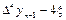
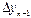
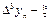
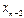
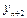
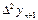
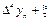
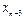
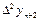
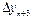
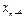
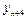
Следует заметить, что максимальная ошибка 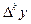– в той же горизонтальной строке, где и табличная величина y_n.

Пример: исправить ошибку в таблице (неверные цифры взяты в скобки).

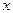
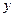
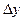
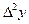
				Ошибка
	13,260
	14,144
	15,912
	15,028		(-4)0
		88(0)4
	16,79(2)6		(8)0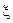
		88(8)4
	17,680		(-4)0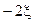
	18,564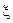
	19,448
	20,332

Как видно из таблицы, ход вторых разностей нарушается при x=19. Ошибка распространяется на 3 строки. Находим среднее арифметическое значение второй разности для средней из 3 точек:

= , =

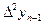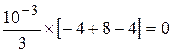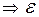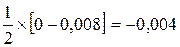
Внося исправление в табличное значение y для x=19, получим верное значение функции:

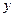_n=(y_n+ 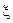)- 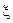=16.792-(-0.004)=16.796.