Интерполяция и экстраполяция
Полученные аналитические зависимости с рассчитанными параметрами позволяют не только выявить тенденцию динамического ряда, но и определить его неизвестные промежуточные значения. Данная задача решается способом интерполяции.
Интерполяция заключается в приближенном отражении сложившейся закономерности внутри определенного отрезка времени – в отличие от экстраполяции, которая требует выхода за пределы этого отрезка времени.
Экстраполяция – метод определения количественных характеристик для совокупностей и явлений, не подвергшихся наблюдению, путем распространения на них результатов, полученных из наблюдения над аналогичными совокупностями за прошедшее время, на будущее.
Формулы для определения значений коэффициентов линейных и нелинейных уравнений, описывающих изменение рассматриваемого показателя во времени и характеризующих тенденцию динамического ряда y=f(t) имеют вид:
Для прямой 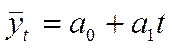
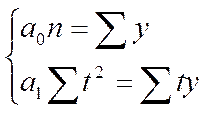
для параболы 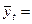
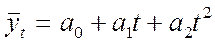
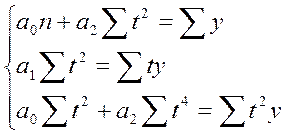
для экспоненты вида 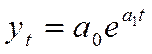
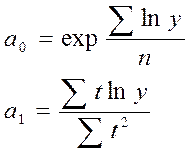
y= b0 + b1/t
система уравнений для определения коэффициентов уравнения регрессии имеет вид:
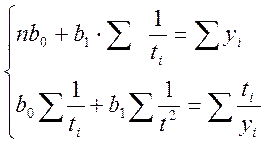
для функции вида 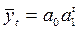
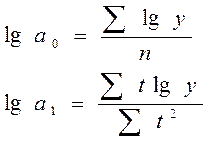
для функции вида 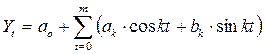
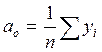
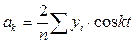
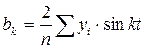
 |  |
Y=a0+a1/x
|
гипербола
 |  |
Y=ax
| |
|
показательная
 | |||
 | |||

ТАБЛИЦА ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ ПО РЯДУ ФУРЬЕ
| t | Yi | cos t | cos 2t | sin t | sin 2t |
| Y1 | |||||
| π/6 | Y2 | 0,866 | 0,5 | 0,5 | 0,866 |
| π/3 | Y3 | 0,5 | -0,5 | 0,866 | 0,866 |
| π/2 | Y4 | -1 | |||
| 2π/3 | Y5 | -0,5 | -0,5 | 0,866 | -0,866 |
| 5π/6 | Y6 | -0,866 | 0,5 | 0,5 | -0,866 |
| π | Y7 | -1 | |||
| 7π/6 | Y8 | -0,866 | 0,5 | -0,5 | 0,866 |
| 4π/3 | Y9 | -0,5 | -0,5 | -0,866 | 0,866 |
| 3π/2 | Y10 | -1 | -1 | ||
| 5π/3 | Y11 | 0,5 | -0,5 | -0,866 | -0,866 |
| 11π/6 | Y12 | 0,866 | 0,5 | -0,5 | -0,866 |
Для изучения сезонности как периодической функции Фурье за n берется число месяцев года, тогда ряд динамики по отношению к значениям определится в виде следующих значений Y (1и2 столбцы).
Дата добавления: 2016-11-02; просмотров: 1797;
