Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на следующем примере.
Для прямой 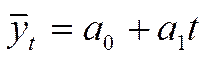
Параметры линейного уравнения определяются из системы уравнения:
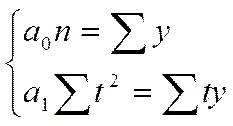
ПРИМЕР: В табл. приведены исходные и расчетные данные о динамике производства молока в регионе за 2009 – 2013 гг.
Таблица : Исходные и расчетные данные для определения параметров системы уравнения
| Годы | Млн.т | t | t2 | tYi | 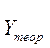
| Yi- 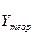
| (Yi- 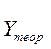 )2 )2
|
| 13,3 | -2 | -26,6 | 13,02 | 0,28 | 0,08 | ||
| 13,5 | -1 | -13,5 | 13,94 | -0,44 | 0,19 | ||
| 14,8 | 14,86 | -0,0 | 0,00 | ||||
| 16,1 | 16,1 | 15,78 | -0,32 | 0,10 | |||
| 16,6 | 33,2 | 16,70 | -0,1 | 0,01 | |||
| Итого | 74,3 | - | 9,2 | 74,30 | - | 0,38 |
Для выравнивания ряда динамики по прямой используем уравнение 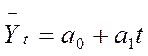
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров 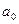 и
и 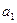 :
:
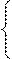
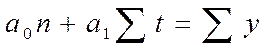

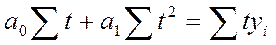
где y – исходный уровень ряда динамики;
N - число членов ряда ;
t – показатель времени, который обозначается порядковыми номерами, начиная с низшего. Например:
Годы 2009 2010 2011 2012 2013
T 1 2 3 4 5
Решение системы уравнений позволяет получить выражения для параметров 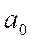 и
и 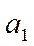 :
:
откуда: 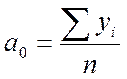 представляет собой средний уровень ряда динамики (
представляет собой средний уровень ряда динамики ( 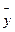 );
);  .
.
Расчет необходимых значений дан в табл. По итоговым данным определяем параметры уравнения:
 ;
;
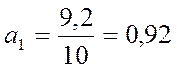 .
.
В результате получаем следующее уравнение основной тенденции производства молока в регионе за 2009 – 2013 гг.
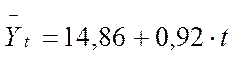 .
.
Подставляя в уравнение принятое обозначение t, вычислим выровненные уровни ряда динамики:
2009 г. - 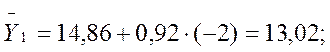
2010 г. - 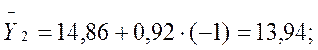 и т.д.
и т.д.
Дата добавления: 2016-11-02; просмотров: 843;
