Способы выравнивания динамических рядов. Экстраполяция и интерполяция
Любой ряд динамики теоретически может включать в себя четыре составляющих: тренд — основная тенденция; циклические, периодические колебания; сезонные колебания; случайные колебания.
Тренд - основная тенденция динамического ряда. Определение основной тенденции развития является важной задачей при изучении рядов динамики. При изучении в рядах динамики основной, тенденции развития применяют различные приемы и способы. Суть этих способов сводится к механическому или аналитическому сглаживанию динамического ряда, что позволяет увидеть тенденцию развития.
Три способа определения тренда:
— метод укрупнения интервалов;
— метод скользящей средней;
— аналитическое выравнивание.
Идея 1-го метода:
Уровни по годам то растут, то падают и не позволяют увидеть: тенденцию. Чтобы ее выявить, переходят к расчету уровней за большие промежутки времени: квартал, год, пятилетка, 10-летис и т.д.
Пример применения метода укрупнения интервалов.
Имеются данные о производстве продукции по месяцам (табл. 5).
Таблица 5
| Месяц года | Производство продукции, млн. руб. |
| январь | |
| февраль | |
| март | |
| апрель | |
| май | |
| июнь | |
| июль | |
| август | |
| сентябрь | |
| октябрь | |
| ноябрь | |
| декабрь |
Рассчитаем по кварталам (табл. 6).
Таблица б
| Квартал | Производство продукции, млн. руб. |
| 1 квартал | |
| 2 квартал | |
| 3 квартал | |
| 4 квартал |
После проведенного укрупнения интервалов четко прослеживается тенденция к увеличению выпуска продукции к концу года.
Идея 2-го метода:
Для каждого уровня определяется средний из близлежащих уровней. Определяют трехзвенную, пятизвенную, семизвенную и т.д. скользящие средние.
В общем виде пятизвенная средняя рассчитывается следующим образом:
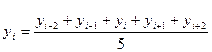
Аналогично рассчитывается трех — и семизвенные средние.
Пример использования метода укрупнения интервалов, проведем сглаживание динамического ряда (табл. 7) при помощи трех и пятизвенной средних. Таблица 7
| Месяцы года | Производство продукции, млн. руб. | Трехзвенная средняя | Пятизвенная средняя |
| январь | - | — | |
| февраль | — | ||
| март | |||
| апрель | |||
| май | |||
| июнь | |||
| июль | |||
| август | |||
| сентябрь | |||
| октябрь | |||
| ноябрь | — | ||
| декабрь | — | — |
Достоинство этого метода — простота и наглядность.
Наиболее эффективным методом выравнивания, является аналитическое выравнивание, так как оно позволяет проводить интерполяцию и экстраполяцию, то есть расчет прогнозных значений на перспективу или ретроспективу.
Идея 3-го метода: представление уровней ряда в виде функции от времени, так как эмпирические точки можно представить в аналитическом виде множеством функций. Подбор функции, соответствующей тенденции, проводится на основе теоретического качественного анализа. При этом необходимо учитывать возможность экономической интерпретации выбранной функции. Три ситуации, интерпретация которых легка:
Ø постоянный абсолютный прирост:
С1= ∆i = Yi - Yi-1 = const
| Y1=1 | 
|
| Y1=2 | yi = a0+a1t |
| Y1=3 |
Ø постоянство вторых абсолютных разностей:
С2= ∆∆i = (Yi - Yi-1) - (Yi-1 – Yi-2) = const
| ∆i | ∆∆i | |
| Y1=1 | - | |
| Y2=4 | ||
| Y3=9 | ||
| Y4=16 | ||
| Y5=25 |
Yt = a0 + a1t + a2t2
Ø постоянный цепной темп роста:
,,3 = Тр = 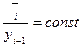
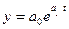 и т.д.
и т.д.
Подбор функции осуществляется также с помощью графического метода (тема «Статистическое изучение взаимосвязей»). Для оценки параметров выбранного уравнения используют любой из трех методов: метод избранных точек, метод наименьших расстояний и метод наименьших квадратов (см. тему «Статистическое изучение взаимосвязей»). Так, например, для прямой yt = а0 + a1t методом наименьших квадратов, получим следующие оценки параметров:
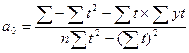
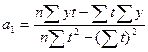
В рядах динамики техника расчета параметров уравнения может быть упрощена. Для этого показателям времени t придают такие значения, чтобы их сумма была равна нулю. В этом случае параметры определяются следующим образом:
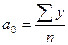
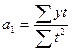
В том случае, если в динамическом ряду нечетное число уровней, то серединное значение времени принимают равным нулю, вверх, по убыванию, располагают по порядку отрицательные значения, вниз, по возрастанию - положительные значения: -5,-4,-3,-2,-1,0,1,2,3,4,5. Если число уровней четное, то строят такой ряд: -7,-5,-3,-1,1,3,5,7-0
Пример использования метода аналитического выравнивания. На основании данных таблицы 5 произведем сглаживание ряда динамики методом аналитического выравнивания (табл. 8):
Таблица 8
| t (месяцы) | y (Производство продукции, млн. руб.) | yt | t2 | (у-уt)2 | yt |
| -11 | -27500 | 36645,44 | 2308,57 | ||
| -9 | -23850 | 55776,30 | 2413,83 | ||
| -7 | -17500 | 364,43 | 2519,09 | ||
| -5 | -12250 | 30397,92 | 2624,35 | ||
| -3 | -7650 | 32259,75 | 2729,61 | ||
| -1 | -2700 | 18189,92 | 2834,87 | ||
| 1610,42 | 2940,13 | ||||
| 2982,25 | 3045,39 | ||||
| 22695,42 | 3150,65 | ||||
| 3125,93 | 3255,91 | ||||
| 68209,77 | 3361,17 | ||||
| 284696,94 | 3466,43 | ||||
| Итого | 556954,49 | 34650,0 |
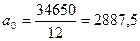
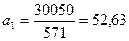
yt = 2887,5 + 52,63t
Интерпретация параметров:
В данном случае а0 - средний уровень ряда, а1 - сила связи, то есть на сколько изменится результат при изменении времени на 1. Для оценки надежности уравнения регрессии применяется критерий Фишера:
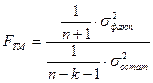
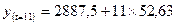
Общая дисперсия:
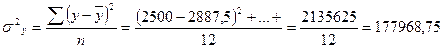
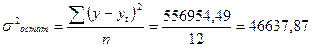
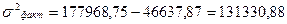
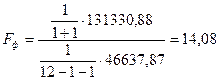
 
| α = 0,05 | |
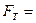
| ϑ1= k +1 =2 | = 4,10 |
| ϑ2= n – k – 1 = 10 |
Fф = 14,08 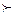 Fт = 4,10
Fт = 4,10 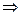 уравнение прямой адекватно отражает имеющийся в данном ряду динамический тренд.
уравнение прямой адекватно отражает имеющийся в данном ряду динамический тренд.
Если построенное уравнение надежно, можно проводить экстраполяцию и интерполяцию.
Экстраполяция — продолжение тенденций прошлого в будущее. Причины ее возникновения:
— инерционность экономических процессов;
— сохранение общих условий и факторов развития процесса.
— отсутствие резких внешних воздействий (война, катастрофа, кризис, землетрясения), способных вызвать скачкообразное изменение.
Экстраполяция может быть реализована на достаточно короткий срок вперед. Для макроэкономических показателей – 5 - 7 лет. Для более частных показателей, наиболее часто подверженных изменениям, - 2 - 3 года.
Экстраполяцию можно провести при помощи точечного прогноза. Точечный прогноз делается по результатам аналитического выравнивания, если уравнение тренда надежно:
ytпр = f (t)
Пример.
Сделаем прогноз производства продукции на 3 месяца вперед:
 t1=13 t1=13
|
| t2=15 |
| t3=17 |
время прогноза - первые три месяца следующего года (январь - 13, февраль - 15, март - 17)
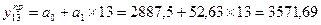
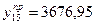
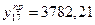
Выводы:
Для комплексного изучения динамики явления необходимо охарактеризовать интенсивность изменения во времени, в том числе в среднем за период; выявить закономерность изменения явления; рассчитать прогнозные значения; определить факторы, формирующие динамику.
Для обеспечения возможности решения задач изучения динамики необходимо при построении динамического ряда выполнять ряд требований.
Для характеристики интенсивности изменения во времени рассчитывают следующие показатели динамики: средний абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Дата добавления: 2016-12-16; просмотров: 2359;
