Правило сложения дисперсии
Если данные представлены в виде аналитической группировки, в статистике рассматривают три вида дисперсии:
— общая дисперсия;
— дисперсия средняя из внутригрупповых;
— межгрупповая дисперсия.
Общая дисперсияизмеряет вариацию признака х во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию.
Межгрупповая дисперсия(факторная) объясняет вариацию, вызванную признаком, положенным в основу группировки. Средняя из внутригрупповых дисперсия(остаточная) объясняет ту часть вариации, которая вызвана действием (влиянием) на признак х всех остальных признаков (факторов), кроме группировочного.
Правило сложения дисперсиизаключается в том, что общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий:
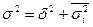 ,
,
где 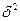 - межгрупповая дисперсия;
- межгрупповая дисперсия;
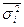 - средняя из внутригрупповых дисперсия.
- средняя из внутригрупповых дисперсия.
Расчет средней из внутригрупповых проводится в два этапа. Первоначально рассчитываются дисперсии по каждой группе, как квадрат отклонений индивидуальных значений признака в группе от средней, рассчитанной в пределах группы:
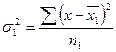 ,
, 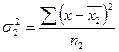 ,
, 
где пi — численность i-ой группы.
На втором этапе по средней арифметической взвешенной рассчитывается средняя из внутригрупповых дисперсия:
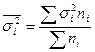
Межгрупповая дисперсия определяется как квадрат отклонений средних, рассчитанных по каждой группе от средней, рассчитанной в пределах всей совокупности, взвешенных численностью группы:
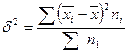
Правильность расчетов дисперсии при помощи правила сложения дисперсии можно подтвердить расчетом общей дисперсии по обычной формуле.
Поскольку правило сложения дисперсии позволяет разложить дисперсию на дисперсию, возникающую под влиянием факторного признака (группировочного), и остаточную дисперсию, оно широко используется при изучении взаимосвязей между признаками.
На основе правила сложения дисперсии в статистике разработаны меры связей между факторным и результативным признаками: коэффициент детерминации и эмпирическое корреляционное отношение.
Коэффициент детерминацииопределяется как отношение межгрупповой дисперсии к общей дисперсии:
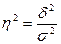 .
.
Коэффициент детерминации характеризует долю общей колеблемости результативного признака, которая вызвана признаком, положенным в основу группировки.
Эмпирическое корреляционное отношениехарактеризует тесноту связи между признаками и определяется следующим образом:
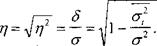
Пример использования правила сложения дисперсии.
Имеются данные о распределении магазинов по объему товарооборота (табл. 3):
Таблица 3
| Товарооборот, тыс. руб. | Число магазинов в группе | Издержки обращения, тыс. руб. |
| 1000—1200 | 20,30,40 | |
| 1200—1500 | 45, 60, 90, 40, 80 | |
| 1500—2500 | 80,85,98,100 |
Определите общую дисперсию, используя правило сложения дисперсии.
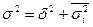
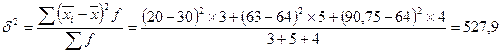
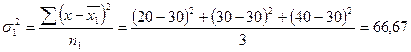
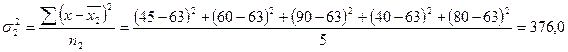
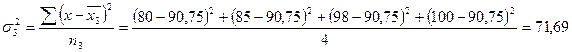
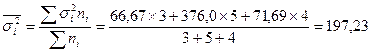
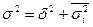 = 527,9 + 197,3 = 725,13
= 527,9 + 197,3 = 725,13
Для проверки правильности расчетов определим общую дисперсию обычным способом:
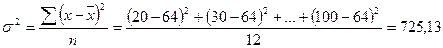
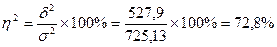
Это значит, что 72,8% вариации издержек обращения объясняется признаком, положенным в основу группировки, то есть товарооборотом. Соответственно, 27,2% вариации результативного признака может быть объяснено прочими факторами, не учтенными в группировке:
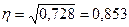
Эмпирическое корреляционное отношение — показатель тесноты связи. Он характеризует уровень согласованности в изменениях факторного признака» (объем товарооборота) и результативного признака (величина издержек обращения).
Эмпирическое корреляционное отношение показывает степень влияния товарооборота на издержки обращения. Иногда дают вероятностную интерпретацию: с вероятностью 0,853 мы можем предсказать изменения издержек обращения, зная изменение товарооборота.
Значения эмпирического корреляционного отношения лежат в диапазоне от 0 до 1: О - 0,3 — слабая связь;
0,3 - 0,7 — умеренная;
0,7 - 1,0 — сильная.
Выводы:
1. Наличие вариации обусловливает необходимость статистики. Статистика изучает только варьирующие явления.
2. Показатели вариации характеризуют однородность совокупности и служат необходимым дополнением при расчете средней величины.
3. Для упрощения расчетов основного показателя вариации — дисперсии — применяют сокращенные способы расчета дисперсии, основанные на свойствах дисперсии.
4. На основании дисперсии (правило сложения дисперсии) рассчитывается эмпирическое корреляционное отношение и коэффициент детерминации, которые служат для характеристики взаимосвязи между признаками.
Дата добавления: 2016-12-16; просмотров: 2014;
