величин. Правило Лопіталя.

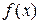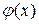Теорема 10.4. Якщо функції і на деякому відрізку 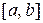задовольняють умови теореми Коші і 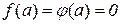, то з існування границі випливає існування границі 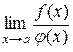, і дві останні рівні, тобто

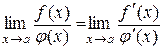. (10.3)

Рівність (10.3) називається правилом Лопіталя.

Доведення. Розглянемо точку і на відрізку запишемо теорему Коші:

,

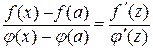де 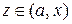. За умовою теореми 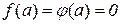, тому остання рівність дає

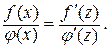. (10.4)

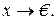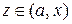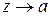Перейдемо в рівності (10.4) до границі при . Оскільки , то при 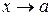. Таким чином,

.

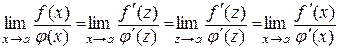Теорема доведена

Наслідок 10.4.1. Попередня теорема має місце й у випадку, коли функці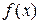ї і 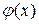не визначені в точці х=а, але

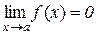і .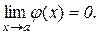

Досить довизначити функці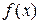ї і 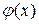в точці 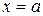, так щоб вони були неперервні, тобто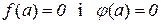

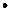
Наслідок 10.4.2. задовольняють

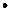
Наслідок 10.4.3. Правило Лопіталя справедливе й у випадку 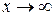, тобто коли ,

.

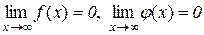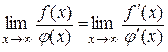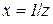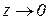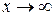Дійсно, нехай , тоді при і

.

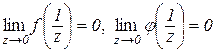Застосувавши правило Лопіталя до відношення 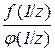, отримаємо

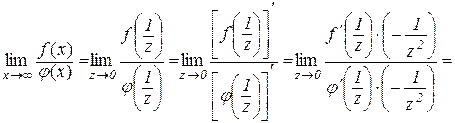
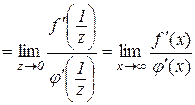
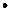
Приклад 10.1.

.

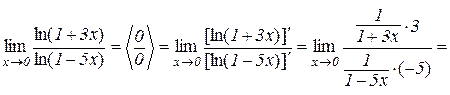
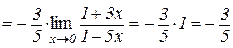Приклад 10.2.

.

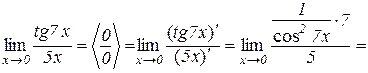
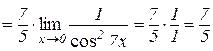Приклад 10.3.

.

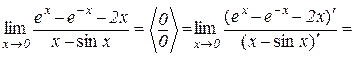
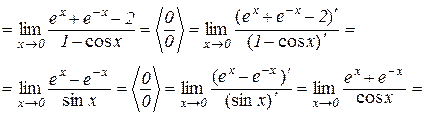
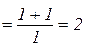Приклад 10.4.

.

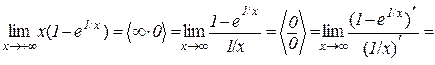
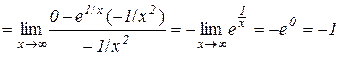10.5.Границя відношення двох нескінченно великих

Функцій.

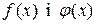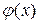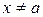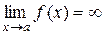Теорема 10.5. Нехай функції і ізнеперервні і диференційовані при всіх з деякого околу точки а, в якому , і нехай і 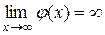. Тоді якщо існує границя

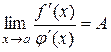, (10.5)

то існує границя 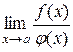і справедлива рівність

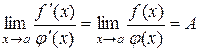. (10.6)

Доведення. В розглядуваному околі точки а виберемо два значення аргументу 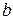і х таких, що 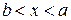( 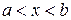). Тоді з теореми Коші слідує

,

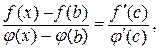де 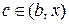або .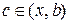

Зробимо тотожні перетворення в останній рівності:

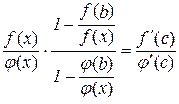
або

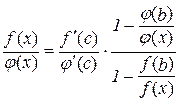. (10.7)

В (10.7) зафіксуємо 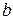і перейдемо до границі при :

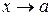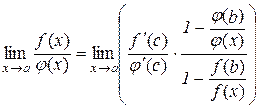(10.8)

Права частина рівності (10.8) дає:

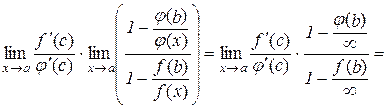
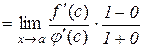. (10.9)

Таким чином, із (10.8), (10.9) отримуємо

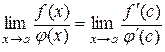. (10.10)

Права частина (10.10) є функцією значення с , яке залежить від вибору числа 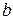. Перейдемо в останній рівності до границі при 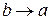. Так як при цьому, очевидно, 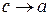, а ліва частина від 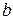не залежить, то отримаємо

.

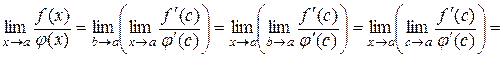
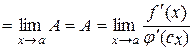Таким чином теорему доведено

Наслідок 10.5.1. Рівність (10.6) справедлива і у випадку, коли .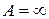

Дійсно, тоді 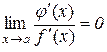і з останньої теореми слідує, що

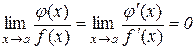або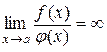

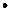
Наслідок 10.5.2. Доведена теорема легко поширюється на випадок .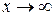

Це слідує з наслідку 10.4.3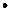

Приклад 10.5.

.

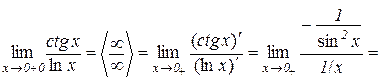
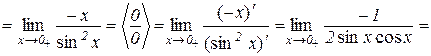
Приклад 10.6.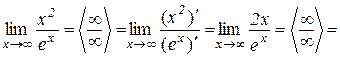

.

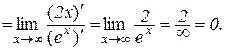За допомогою двох останніх теорем можна також розкривати невизначеності типу .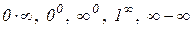

Приклад 10.7. Знайти границю

.

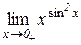Розв’язування. Нехай

,

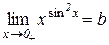тоді

.

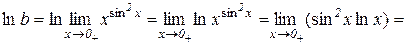
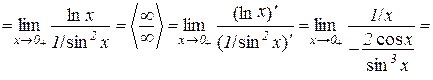
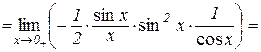
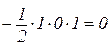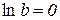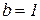Таким чином, або і .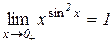

10.6.Формули Тейлора і Маклорена.

Припустимо, що в деякому околі точки а функція 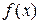має всі похідні до (n+1)-го порядку. Знайдемо такий многочлен 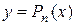, який в точці 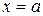набуває значення 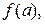, а всі його похідні до n-го порядку в цій точці рівні значенням відповідних похідних функції 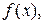, тобто

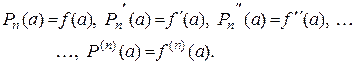(10.11)

Многочлен будемо шукати у вигляді многочлена за степенями двочлена х-а:

. (10.12)

Коефіцієнти С₀ , С₁ , С₂ , ..., С_n треба підібрати такими, щоб виконувалась умова (10.11).

Знайдемо похідні многочлена :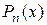

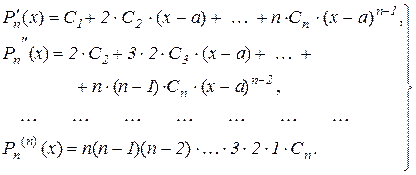(10.13)

З (10.11)–(10.13) маємо:

або

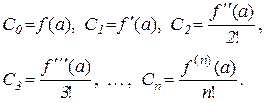(10.14)

Підставивши (10.14) в (10.12), отримаємо

Нехай 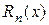– різниця між значеннями заданої функції і многочлена , тобто 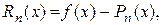, тоді

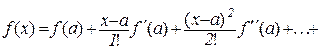
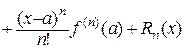. (10.15)

Означення 10.1. Функція 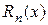називається залишковимчленом.

Проведемо оцінку залишкового члена. Для цього представимо його у вигляді

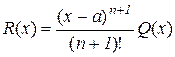, (10.16)

де 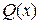– невідома функція, яку потрібно знайти.

Підставимо (10.16) в (10.15)

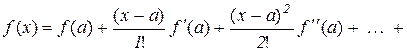
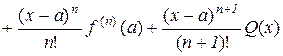, (10.17)

і розглянемо допоміжну функцію :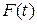

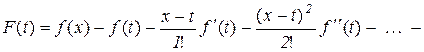
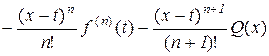, (10.18)

де t лежить в проміжку між а і х.

Знайдемо :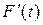

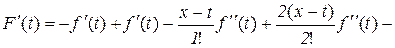
або після скорочення

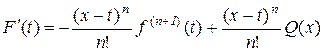. (10.19)

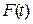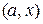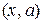Таким чином, з рівностей (10.17)–(10.19) слідує, що функція неперервна і диференційована на або та 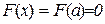, тобто для даної функції справедлива теорема Ролля: 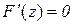, де z розміщене між а і х. З (10.19) отримуємо, що

і залишковий член 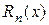можна подати у вигляді

,

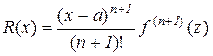який називають формою Лагранжа для залишкового члена.

Іколи застосовують запис 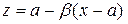, де 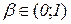, і залишковий член набирає вигляду

.

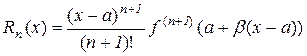Таким чином, ми отримали формулу

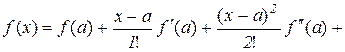
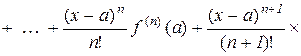
, (10.20)

яка називається формулою Лагранжа для функції .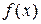

Частинний випадок формули (10.20) при 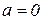, тобто

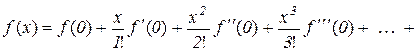
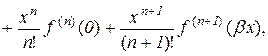(10.21)

називається формулою Маклорена.

10.7.Розклад за формулою Маклорена функцій

.

1. Для функції 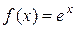маємо

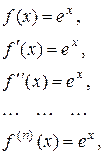
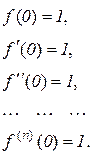
і формула (10.21) набирає вигляду

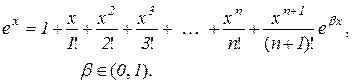(10.22)

2. Нехай 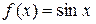, тоді

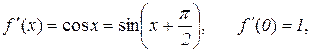
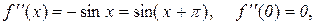
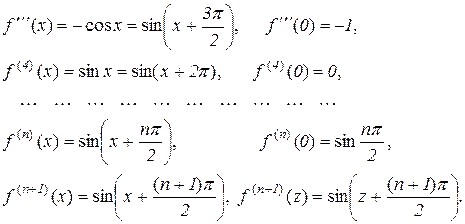
Таким чином,

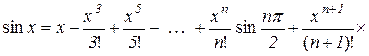
. (10.23)

3. Аналогічно можна записати формулу (10.17) для функції :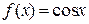

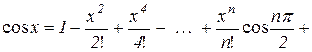
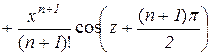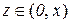, . (10.24)

Приклад 10.8. Обчислити 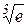з точністю до 0,001.

Розв’язування. Використаємо формулу (10.22) – розклад функції 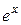за Маклореном. В нашому прикладі 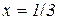, тому залишковий член можна оцінити наступним чином

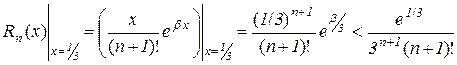
або

.

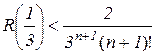Знайдемо n, при якому залишковий член не перевищує значення 0,001:

; ;

; .

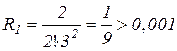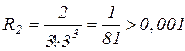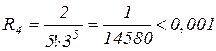Отже, в формулі Маклорена досить взяти п’ять перших доданків, щоб отримати значення 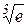з точністю до 0,001:

.

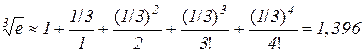Запитання для самоконтролю.

1. Сформулюйте і доведіть теорему Ролля.

2. Дайте геометричне тлумачення теореми Ролля.

3. Сформулюйте й доведіть теорему Лагранжа.

4. Дайте геометричне тлумачення теореми Лагранжа.

5. Сформулюйте і доведіть теорему Коші.

6. Виведіть правило Лопіталя.

7. Які ви знаєте наслідки правила Лопіталя?

8. Як розкривати невизначеності типу , ?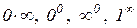

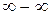9. Запишіть формули Тейлора і Маклорена.

10. Що таке залишковий член і форми його запису?

11. Запишіть формули Маклорена для функцій .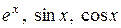

Приклади до розділу 10.

1. Показати, що між коренями функції 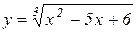міститься корінь її похідної.

2. Функція 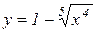дорівнює нулю при 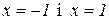. Показати, що на інтервалі її похідна не рівна нулю.

3. Перевірити справедливість формули Лагранжа для функції 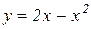на відрізку .

4. Записати формулу Коші для функцій 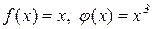на відрізку 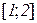і знайти с. Відп.: с=14/9.

5. Знайти границі:

а) 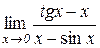Відп.: 2. б) 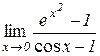. Відп.: –2.

в) 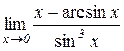. Відп.: –1/6. г) 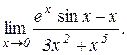. Відп.: 1/3.

д) . Відп.: 1. е) . Відп.: 0.

6. Знайти границі:

а) 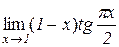. Відп.: 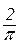. б) 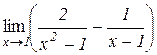. Відп.: .

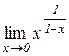в) . Відп.: –1. г) . Відп.: .

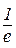д) 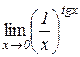. Відп.: 1. е) 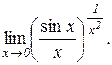. Відп.: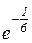

7. Розкласти за степенями двочлена 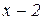многочлен

.

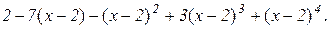8. Записати формулу Маклорена для функції 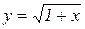, якщо .

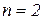9. Знайти 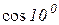з точністю до 0,001.