ВИДЫ ДИСПЕРСИИ. ПРАВИЛО СЛОЖЕНИЯ ДИСПЕРСИЙ

Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку.

Тогда наряду с изучением вариации признака по всей совокупности в целом, становиться возможным изучать вариацию для каждой из составляющих ее групп, а также между этими группами.

В простейшем случае, когда совокупность расчленена на группы по однородному фактору, изучение вариации достигается посредством расчета и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.

Общая дисперсия ( 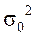) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

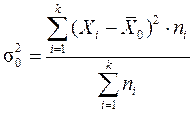
Межгрупповая дисперсия ( 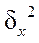) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под действием признака-фактора, положенного в основу группировки.

;

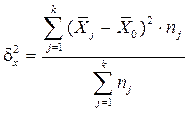где 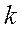- число групп;

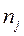- число единиц в j-й совокупности;

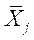- частная средняя по j-й группе;

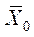- общая средняя по совокупности единиц.

Внутригрупповая дисперсия ( 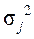) отражает случайную вариацию, т.е. часть вариации, происходящей под влиянием неучтенных факторов и не зависящую от признака-фактора.

.

По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий ( ):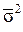

.

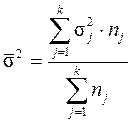Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

.

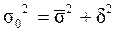Эмпирический коэффициент детерминации – доля межгрупповой дисперсии в общей дисперсии.

.

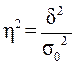Эмпирическое корреляционное отношение – корень квадратный из эмпирического коэффициента детерминации (если 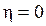, то группировочный признак не оказывает влияния на результативный; если же 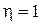, то результативный признак изменяется только в зависимости от признака, положенного в основу группировки, а влияние прочих факторных признаков равно нулю):

.

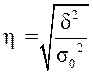Для проверки существенности связи между группировочным признаком и вариацией исследуемого признака часто используется дисперсионное отношение 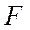(критерий Фишера).

,

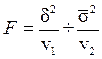где 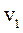, 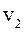- число степеней свободы для сравниваемых дисперсий,

при этом ;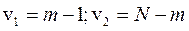

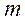- число групп;

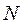- число наблюдений.

Расчетное значение критерия Фишера ( 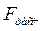) сравнивается в критическим ( 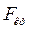), которое определяется по таблице; если 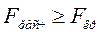, наличие связи доказано.

Эмпирическое корреляционное отношение может принимать значение от 0 до ±1.

Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.

Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии, т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.

Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимость между признаками.

Для качественной оценки степени тесноты связи на основе показателей тесноты связи можно воспользоваться шкалой Чэддока.

Таблица 4.2

Шкала Чэддока