ДИСПЕРСИЯ, ЕЕ СВОЙСТВА И МЕТОДЫ РАСЧЕТА
Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины и в зависимости от исходных данных вычисляется по формулам:
Для альтернативных признаков: 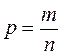 - доля единиц совокупности, обладающих данным признаком;
- доля единиц совокупности, обладающих данным признаком; 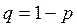 - доля единиц, не обладающих данным признаком. Дисперсия альтернативного признака:
- доля единиц, не обладающих данным признаком. Дисперсия альтернативного признака: 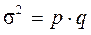 .
.
Для количественных признаков:
- простая дисперсия 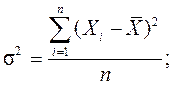
- взвешенная дисперсия 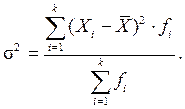
Дисперсия обладает рядом свойств:
1. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится: s
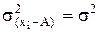 .
.
2. Если все значения вариант разделить на какое-то по постоянное число А, то дисперсия уменьшится от этого в А2 раз, а среднее квадратическое отклонение - в А раз:
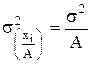 .
.
3. Если исчислить дисперсию от любой величины А, которая отличается от средней арифметической 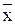 , то эта дисперсия всегда будет больше дисперсии, исчисленной от средней арифметической
, то эта дисперсия всегда будет больше дисперсии, исчисленной от средней арифметической 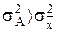 . При этом больше на вполне определенную величину - квадрат разности между средней и условно взятой величиной А, т.е. на
. При этом больше на вполне определенную величину - квадрат разности между средней и условно взятой величиной А, т.е. на 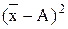 :
: 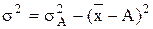 .
.
Исходя из этих свойств, дисперсия для интервального вариационного ряда с равными интервалами определяется способом моментов по формуле:
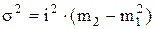 ,
,
где i - величина интервала;
m12 - момент первого порядка в квадрате;
m2- момент второго порядка.
Для интервального вариационного ряда распределения среднее квадратическое отклонение способом моментов определяется по формуле:
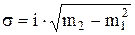 ,
,
где i – величина интервала;
m1 - момент первого порядка 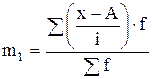 ;
;
m2 - момент второго порядка 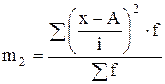 .
.
Дата добавления: 2016-05-25; просмотров: 2744;
