ВАРИАЦИЯ ПРИЗНАКА И ПОКАЗАТЕЛИ ЕЕ ОЦЕНКИ
Вариация – колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

Рис. 1. Факторная классификация вариаций

Рис. 2. Классификация показателей вариации признака
Абсолютные показатели вариации – это размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и дисперсия.
Относительные показатели вариации – это коэффициенты осцилляции, вариации, относительное линейное отклонение и др.
Средняя арифметическая:
- для первичного ряда (простая средняя арифметическая):
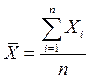 ;
;
- для ранжированного вариационного ряда (взвешенная средняя арифметическая):
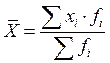 .
.
Мода и медиана – структурные средние.
Мода 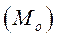 – значение изучаемого признака, повторяющееся с наибольшей частотой.
– значение изучаемого признака, повторяющееся с наибольшей частотой.
Для интервального распределения с равными интервалами:
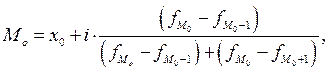
где
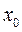 - нижняя граница модального интервала;
- нижняя граница модального интервала;
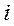 - величина модального интервала;
- величина модального интервала;
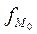 - частота модального интервала;
- частота модального интервала;
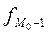 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
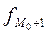 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Модальное значение является валидной мерой центральной тенденции асимметричного распределения социально-экономических показателей.
Для интервального распределения с неравными интервалами:
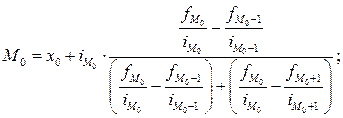
где
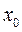 - начальная граница модального интервала, в котором достигает максимума величина
- начальная граница модального интервала, в котором достигает максимума величина 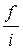 - отношение частоты интервала к его величине;
- отношение частоты интервала к его величине;
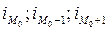 - величина соответствующего модального, до- и послемодального интервалов;
- величина соответствующего модального, до- и послемодального интервалов;
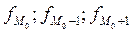 - частота модального, до- и послемодального интервалов соответственно.
- частота модального, до- и послемодального интервалов соответственно.
Медиана 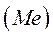 – значение признака, приходящееся на середину ранжированной совокупности. Структурные средние могут быть определены по дискретным и интервальным рядам распределения.
– значение признака, приходящееся на середину ранжированной совокупности. Структурные средние могут быть определены по дискретным и интервальным рядам распределения.
Формулы для исчисления медианы вариационного ряда:
- при нечетном числе вариантов - 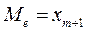 ;
;
- при четном числе вариантов - 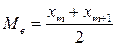 .
.
Формула для исчисления медианы интервального ряда:
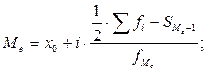
где
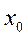 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
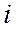 - величина медианного интервала;
- величина медианного интервала;
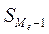 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному;
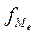 - частота медианного интервала.
- частота медианного интервала.
Размах вариации ( 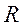 ) – разность между наибольшим и наименьшим значениями варьирующего признака.
) – разность между наибольшим и наименьшим значениями варьирующего признака.
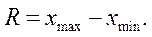
Среднее линейное отклонение – средняя арифметическая из абсолютных значений отклонений вариант признака от их средней. Эта величина вычисляется как средняя арифметическая из абсолютных значений отклонений вариант 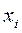 и
и 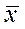 :
:
простая - 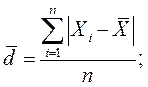
взвешенная – 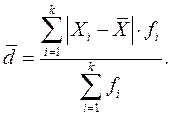
Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины и в зависимости от исходных данных вычисляется по формулам:
- простой дисперсии – 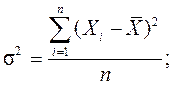
- взвешенной дисперсии - 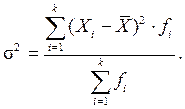
Среднее квадратическое отклонение (нормированное или стандартизированное отклонение) рассчитывается как корень квадратный из дисперсии. Оно может быть:
- простым - 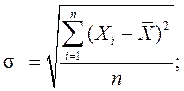
- взвешенным - 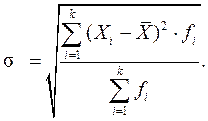
Дата добавления: 2016-05-25; просмотров: 1038;
