Абсолютные и относительные показатели вариации и способы их расчёта.

Вариационныминазывают ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее различаются между собой.

Вариация- колеблемость, изменяемость величины признака у единиц совокупности. Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантамизначений. Недостаточность средней величины для полной характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака.

Наличие вариации обусловлено влиянием большого числа факторов на формирование уровня признака. Эти факторы действуют с неодинаковой силой и в разных направлениях. Для описания меры изменчивости признаков используют показатели вариации.

Задачи статистического изучения вариации:

1) изучение характера и степени вариации признаков у отдельных единиц совокупности;

2) определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности.

В статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, с помощью которых измеряется вариация.

Исследование вариаций имеет важное значение. Измерение вариаций необходимо при проведении выборочного наблюдения, корреляционном и дисперсионном анализе и т. д.

По степени вариации можно судить об однородности совокупности, об устойчивости отдельных значений признаков и типичности средней. На их основе разрабатываются показатели тесноты связи между признаками, показатели оценки точности выборочного наблюдения.

Различают вариацию в пространстве и вариацию во времени.

Под вариацией в пространстве понимают колеблемость значений признака у единиц совокупности, представляющих отдельные территории. Под вариацией во времени подразумевают изменение значений признака в различные периоды времени.

Для изучения вариации в рядах распределения проводят расположение всех вариантов значений признака в возрастающем или убывающем порядке. Этот процесс называют ранжированием ряда.

Самыми простыми признаками вариации являются минимум и максимум- самое наименьшее и наибольшее значение признака в совокупности. Число повторений отдельных вариантов значений признаков называют частотой повторения (fi). Частоты удобно заменять частостями – wi. Частость - относительный показатель частоты, который может быть выражен в долях единицы или процентах и позволяет сопоставлять вариационные ряды с различным числом наблюдений. Выражается формулой:

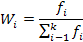
Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. К относительным показателям колеблемости относят коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации.

Размах вариации. Среднее линейное отклонение

Абсолютные и средние величины не могут дать всесторонней характеристики изучаемой совокупности, не позволяют судить о структуре совокупности, о внутреннем ее строении. Более полное представление об изучаемой совокупности может быть получено путем исследования различий между единицами совокупности с помощью измерения колеблемости изучаемого признака.

Размах вариации(R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности (R = Хmax- Xmin). Этот показатель дает самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Зависимость от крайних значений признака придает размаху вариации неустойчивый, случайный характер.

Размах вариации не связан с частотами в вариационном ряду. т. е. с характером распределения. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних. Область применения этого показа-геля ограничена достаточно однородными совокупностями.

Для характеристики вариации признака нужно знать не только амплитуду (размах) его значений, но и уметь обобщить отклонения всех этих значений от какой-либо типичной для изучаемой совокупности величины. В качестве такой величины используют среднюю арифметическую. Такие показатели вариации, пак среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. основаны на рассмотрении отклонений значений признака Отдельных единиц совокупности от средней арифметической.

Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

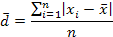
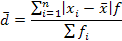
где d - среднее линейное отклонение;

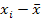| | - абсолютное значение (модуль) отклонения варианта от средней арифметической;

f-частота.

Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая - в рядах с неравными частотами. Необходимость использования в формулах среднего линейного отклонения модулей отклонений вариантов от средней вызвана тем, что алгебраическая сумма этих отклонений равна нулю по свойствам средней арифметической. Среднее линейное отклонение показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.

Дисперсия. Виды дисперсий

Дисперсия ( 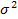) - средняя из квадратов отклонений вариантов значений признака от их средней величины:

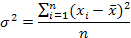
Или 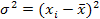для не сгруппированных данных,

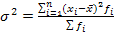для сгруппированных данных.

Свойства дисперсии.

1. Дисперсия постоянной величины равна 0.

2. Уменьшение всех значений признака на одну и ту же величину не изменяет величину дисперсии:

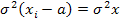
3. Уменьшение всех значений признака в к раз уменьшает дисперсию в k2 раз: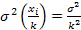

4. Средний квадрат отклонений, исчисленный от среднего арифметического, всегда будет меньше среднего квадрата отклонений, исчисляемого от любой другой величины: 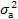> 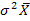. Величина различия между ними вполне определенная, это квадрат разности между средней и этой условной величиной А.

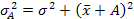
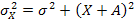
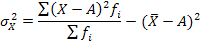
Дисперсия альтернативного признака, т. е. признака, имеющего два противоположных значения. В таких случаях наличие признака обозначается единицей, а его отсутствие - нулем. Доля единиц, обладающих признаком, обозначается через р, доля остальных единиц - q= 1 - р. Средняя величина альтернативного признака:

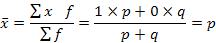
Дисперсия альтернативного признака:

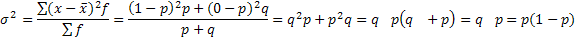
Cреднее квадратическое отклонение альтернативного признака:

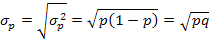
Общая дисперсия измеряет вариацию признака во всей совокупности, возникающую под влиянием всех факторов. Исчисляется по формуле:

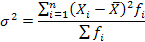
Групповые средние и дисперсии обозначим соответственно х. и о'. Внутригрупповые дисперсии показывают величину вариации, вызванную всеми признаками, кроме признака, положенного в основу группировки.

Межгрупповая дисперсия является мерой вариации признака между группами и характеризует колеблемость групповых средних (Т) около общей средней (Т) (среднее квадратическое отклонение групповых средних от общей средней):

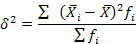
Среднее квадратическое (стандартное) отклонение. Коэффициент вариации

Среднее квадратическое отклонение основано на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической. При этом используется способ усреднения отклонений вариантов от средней арифметической, позволяющий обойти трудность, обусловленную равенством нулю их алгебраической суммы. Данный способ сводится к расчету квадратов отклонений вариантов от средней с их последующим усреднением.

Дисперсия (о*) - средняя из квадратов отклонений вариантов значений признака от их средней величины:

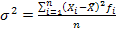
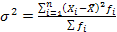
вторая формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).

Среднее квадратическое отклонение ˚ представляет собой корень квадратный из дисперсии:

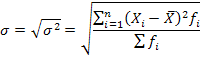
Среднее квадратическое отклонение показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.

В статистической практике часто возникает необходимость сравнения вариации различных признаков. При сравнении изменчивости различных признаков в совокупности, для оценки интенсивности вариации, для сравнения ее в разных совокупностях 1 и для разных признаков удобно применять относи - тельные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости:

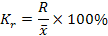
(коэффициент осцилляции);

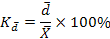
(относительное линейное отклонение).

Коэффициент вариации- наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному. Коэффициент вариации применяется для сравнения колеблемости разнородных признаков. Коэффициент вариации часто используется для сравнения размеров вариации в совокупностях, отличающихся друг от друга величиной средней (в совокупностях с разными уровнями):

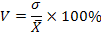
Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава. При этом при равенстве коэффициентов вариации для различных признаков или в разных совокупностях вариация в одних случаях может считаться как сильная, а в других - как слабая. Различная сила, интенсивность вариации обусловлены объективными причинами.