Вопрос № 17. Дисперсия и её виды. Правило сложения дисперсий.

Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от средней величины.

Дисперсия имеет ряд математических свойств, упрощающих технику ее расчета.

1.Если из всех вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится.

2.Если все значения вариант разделить на какое-то постоянное число h, то дисперсия уменьшится от этого в h2раз, а среднее квадратическое отклонение – в h раз.

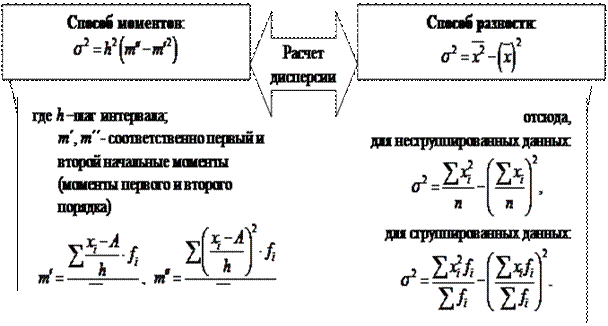
Методика расчета показателя дисперсии упрощенными способами показана на рис. 5.4. Отметим, что способ моментов применим в том случае, если задан интервальный ряд с равными интервалами, а способ разности применяется в любых рядах распределения: дискретных и интервальных с равными и неравными интервалами.

Вариация признака определяется различными факторами, в результате чего различают общую дисперсию, межгрупповую дисперсию и внутригрупповую дисперсию.

Общая дисперсия(σ2) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.

Межгрупповая дисперсия(σ2м.гр) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки.

Рис.5.4. Упрощенные способы расчета дисперсии

,

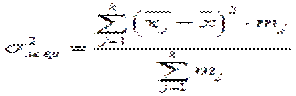где k – количество групп, на которые разбита вся совокупность;

mj – количество объектов, наблюдений, включенных в группу j;

– среднее значение признака по группе j;

– общее среднее значение признака.

Внутригрупповая дисперсия(σ2j,вн.гр) отражает случайную вариацию, т.е. часть вариации, возникающую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.

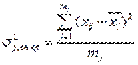, или, на основе метода разностей ,

где xij – значение i-ой варианты в группе j.

Если в сформированных группах отдельные данные встречаются не один раз, то для расчета внутригрупповой дисперсии используется формула средней арифметической взвешенной.

Среднее значение внутригрупповых дисперсийрассчитывается по формуле:

.

Существует закон согласно которому, общая дисперсия, возникающая под воздействием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака и дисперсии, появляющейся под влиянием всех прочих факторов. Этот закон связывает три вида дисперсии.

Правило сложения дисперсий: .

Правило сложения дисперсии широко применяется при исчислении тесноты связей между признаками (факторным и результативным). Для этого определяют эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.

Эмпирический коэффициент детерминации(η2) показывает, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки. (η – греческая буква «эта»).

.

Эмпирическое корреляционное отношение(η) показывает тесноту связи между признаками - группировочным и результативным.

.

Оно изменяется в пределах от 0 до 1. Если η = 0, то группировочный признак не оказывает влияния на результативный, если η =1,то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторов равно нулю. Характеристика связи между признаками при соответствующих значениях эмпирического корреляционного отношения приведена в табл. 5.7.

Таблица 5.7

Качественная оценка связи между признаками