Понятие, способы определения.
Для характеристики среднего значения признака в вариационном ряду применяются: средняя арифметическая, медиана, мода.
Средняя арифметическая — одна из наиболее распространенных, применяется в тех случаях, когда объем варьирующего признака для всей совокупности есть сумма индивидуальных значений ее отдельных элементов. Для не сгруппированных данных вычисляют среднюю арифметическую простую, для сгруппированных — взвешенную.
Средняя арифметическаядля дискретных и интервальных рядов распределения исчисляется по формуле:
 (5.9)
(5.9)
где  — варианты значений признака.
— варианты значений признака.
В случае непрерывного значения признака в качестве принимается середина соответствующего интервала и вычисляется как средняя из значений границ интервала.
Медиана (Ме) — варианта, которая делит ранжированный ряд на две, равные по численности, части. Так, если в ряду распределения рабочих по возрасту Ме = 34, то это означает, что половина из них меньшие этого возраста, половина — старшие этого возраста. Если ряд содержит парное число членов, медиана равняется средний из двух значений расположенных внутри ряда. Для нахождения медианы в дискретном ряду сначала вычисляют полусумму частот, а потом определяют, какая варианта приходится на нее. Для интервального ряда медиану вычисляют по формуле где - нижняя граница медианного интервала; — размер медианного интервала; полусумма частот медианного интервала; — сумма накопленных частот перед медианным интервалом; — частота медианного интервала.
Медиана (Me)соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером:
 , (5.10)
, (5.10)
где n — число единиц в совокупности.
По накопленным частоcтям определяют ее местоположение и численное значение в дискретном вариационном ряду.
Если совокупность содержит четное число значений варьирующего признака (n = 2k; k = n/2), то в этом случае за медиану условно принимают значение
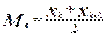 , (5.11)
, (5.11)
так как в ряду нет члена, который делил бы совокупность на две равные по объему группы.
В интервальном ряду распределения сначала указывают интервал, в котором находится медиана.
Медианным является первый интервал, в котором сумма накопленных частостей превысит 0,5.
Мода (Мо) — значение варианты, которое чаще повторяется в ряду распределения. В дискретном ряду моду легко отыскать визуально, в интервальном ряду легко отыскать модальный интервал, а приблизительное значение моды исчисляется по формуле - нижняя граница модального интервала; — размер модального интервала; - частота модального интервала; - частота предшествующего интервала; частота интервала, следующего за модальным.
Мода (Мо)— наиболее часто встречающееся значение признака. В дискретном ряду — это варианта с наибольшей частотой. В интервальном ряду сначала определяется модальный интервал, т. е. тот интервал, который имеет наибольшую частоту (частость).
Численное значение моды и медианы определяется по формулам:
 (5.12)
(5.12)
 (5.13) где
(5.13) где  - нижние границы модального и медианного интервалов;
- нижние границы модального и медианного интервалов;
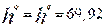 - ширина модального и медианного интервалов;
- ширина модального и медианного интервалов;
 - частость модального интервала;
- частость модального интервала;
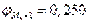 - частость интервала, предшествующему модальному;
- частость интервала, предшествующему модальному;
 - частость интервала следующего за модальным;
- частость интервала следующего за модальным;
 - половина суммы накопленных частостей (равна 0,5);
- половина суммы накопленных частостей (равна 0,5);
 - накопленная частость до медианного интервала;
- накопленная частость до медианного интервала;
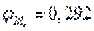 - частость медианного интервала.
- частость медианного интервала.
Моду и медиану можно определить на основе графического изображения ряда. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной.
Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника — с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.
Дата добавления: 2016-06-24; просмотров: 1239;
