Вопрос № 20.Параметрические методы определения тесноты и направления связи: линейный коэффициент корреляции, эмпирическое корреляционное отношение
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIXв. Пирсоном, Эджвортом и Велдоном и характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формул расчета данного коэффициента:
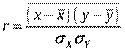
Используя математические свойства средней, получаем:
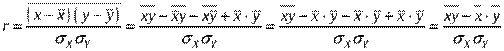
Преобразования данной формулы позволяют получить следующую формулу линейного коэффициента корреляции:
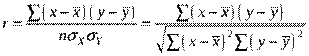
где 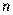 – число наблюдений.
– число наблюдений.
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
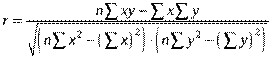
Коэффициент корреляции может быть выражен через дисперсии слагаемых:
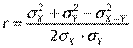
Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Легко доказывается, что условие 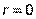 является необходимым и достаточным для того, чтобы величины
является необходимым и достаточным для того, чтобы величины 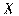 и
и 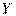 были независимы.
были независимы.
Если же 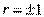 , то это означает, что все точки
, то это означает, что все точки 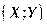 находятся на прямой и зависимость между и является функциональной. Указанное положение распространяется также на случай нормального распределения трех и более величин.
находятся на прямой и зависимость между и является функциональной. Указанное положение распространяется также на случай нормального распределения трех и более величин.
Линейный коэффициент корреляции изменяется в пределах от –1 до 1 : 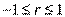 .
.
Дата добавления: 2016-06-24; просмотров: 1235;
