ДИФЕРЕНЦІЙОВАНІ ФУНКЦІЇ.
ДЕЯКІ ТЕОРЕМИ ПРО
 10.1.Теорема про корені похідної.
10.1.Теорема про корені похідної.
Теорема 10.1 (Ролля). Якщо функція 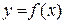 задовольняє умови:
задовольняє умови:
а) неперервна на відрізку 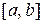 ;
;
б) диференційована на інтервалі  ;
;
в) 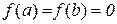 ,
,
то існує хоча б одна точка 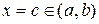 така, що
така, що 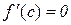 .
.
Доведення. З умови а) та теореми 5.2 випливає, що на відрізку 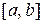 функція
функція 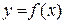 набуває свого найбільшого М та найменшого m значень. Якщо m=M, то f(x) стала, тобто
набуває свого найбільшого М та найменшого m значень. Якщо m=M, то f(x) стала, тобто  для будь-якого
для будь-якого 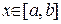 , і
, і 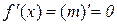 . Отже, теорему доведено.
. Отже, теорему доведено.
Припустимо, що 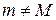 . Тоді хоча б одне з чисел m або M відмінне від нуля. Нехай М>0 і функція
. Тоді хоча б одне з чисел m або M відмінне від нуля. Нехай М>0 і функція 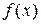 набуває свого найбільшого значення при х=с, тобто
набуває свого найбільшого значення при х=с, тобто 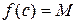 . З умови в) виходить, що
. З умови в) виходить, що 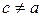 і
і 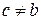 .
.
Оскільки 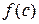 – найбільше значення функції, то
– найбільше значення функції, то 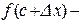
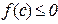 як при
як при 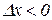 , так і при
, так і при 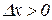 . Таким чином,
. Таким чином,
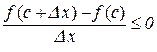 , при
, при  ; (10.1)
; (10.1)
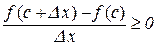 , при
, при 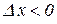 . (10.2)
. (10.2)
Перейдемо в (10.1), (10.2) до границі при 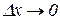 з урахуванням умови б) нашої теореми і теореми 3.10:
з урахуванням умови б) нашої теореми і теореми 3.10:
 при
при 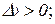 ;
;
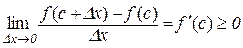 при
при 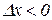 .
.
Але співвідношення 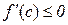 і
і 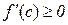 сумісні тільки при
сумісні тільки при  , тобто теорему доведено
, тобто теорему доведено 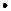
Наслідок 10.1. Попередня теорема справедлива і у випадку, коли умову в) замінити на – 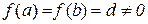 .
.
Дійсно, тепер для функції  виконуватимуться всі умови теореми Ролля, а значить, існує точка
виконуватимуться всі умови теореми Ролля, а значить, існує точка 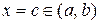 така, що
така, що 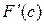
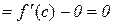
Геометричний зміст теореми Ролля показано на рис.10.1. Якщо лінія в кожній точці інтервалу  має дотичну і на кінцях цього інтервалу набуває однакових значень, то в середині цього відрізка існує хоча б одна точка с, в якій дотична паралельна осі ОХ.
має дотичну і на кінцях цього інтервалу набуває однакових значень, то в середині цього відрізка існує хоча б одна точка с, в якій дотична паралельна осі ОХ.
10.2.Теорема про скінченні прирости.
Теорема 10.2 (Лагранжа). Якщо функція  задовольняє умови:
задовольняє умови:
а) неперервна на відрізку 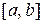 ;
;
б) диференційована на інтервалі  ,
,
то існує хоча б одна точка 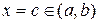 така, що
така, що
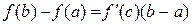 або
або 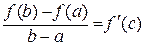 .
.
Доведення. Нехай
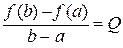 .
.
Розглянемо допоміжну функцію 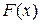 :
:
 .
.
Вона задовольняє всі умови теореми Ролля. Справді, 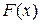 – неперервна і диференційована як сума неперервних й диференційованих функцій та
– неперервна і диференційована як сума неперервних й диференційованих функцій та
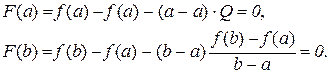
Таким чином, існує точка 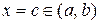 така, що
така, що 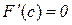 . Але
. Але
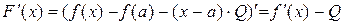 ,
,
тому
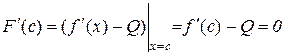
або
 .
.
Теорему доведено 
Геометричне тлумачення теореми Лагранжа показане на рис. 10.2. Якщо лінія  неперервна і в кожній точці інтервалу
неперервна і в кожній точці інтервалу  має дотичну, то існує хоча б одна точка
має дотичну, то існує хоча б одна точка 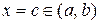 така, що дотична в ній паралельна хорді, проведеній через точки
така, що дотична в ній паралельна хорді, проведеній через точки 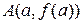 і
і 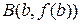 .
.
Дата добавления: 2016-05-05; просмотров: 941;
