Перетворення Лежандра. Нерівність Юнга. Двоїсті за Юнгом функції. Теорема Донкіна. Теореми Лагранжа і Кастільяно
Перетворення Лежандра – допоміжний математичний прийом, який полягає у переході від функцій на лінійному просторі до функцій на спряженому просторі. Воно аналогічно проективній подвійності і тангенціальним координатам у алгебраїчній геометрії або побудові спряженого банахова простору в математичному аналізі.
Нехай 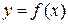 опукла,
опукла, 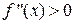 .
.
Перетворення Лежандра функції 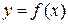 називається нова функція
називається нова функція 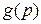 нового змінного, яка будується наступним чином:
нового змінного, яка будується наступним чином:
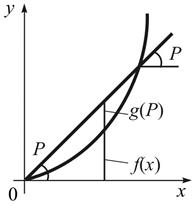 Рис. 7.1
Рис. 7.1
| 1. 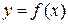 2.
2. 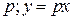 3.
3. 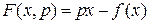 4.
4. 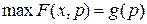 5.
5. 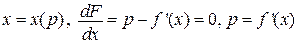 6.
6. 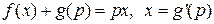
|
Дві функції 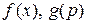 , які являють собою перетворення Лежандра одна до одної, називаються двоїстими за Юнгом. За визначенням перетворення Лежандра
, які являють собою перетворення Лежандра одна до одної, називаються двоїстими за Юнгом. За визначенням перетворення Лежандра 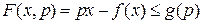 , звідки витікає нерівність Юнга
, звідки витікає нерівність Юнга
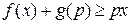 .
.
Теорема. Перетворення Лежандра інволютивне, тобто його квадрат дорівнює тотожному перетворенню: якщо 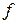 при перетворенні Лежандра переходить в
при перетворенні Лежандра переходить в 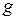 , то перетворення Лежандра від
, то перетворення Лежандра від 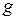 буде знову
буде знову 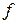 .
.
Доведення. Щоб здійснити перетворення Лежандра функції 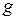 змінного
змінного 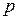 , миповинні, за визначенням, розглянути нове незалежне змінне (позначимо його через
, миповинні, за визначенням, розглянути нове незалежне змінне (позначимо його через 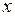 , скласти функцію
, скласти функцію
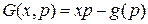 ,
,
знайти точку 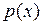 , в якій
, в якій 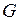 має максимум:
має максимум:
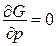 , тобто
, тобто 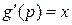 ,
,
і тоді перетворення Лежандра 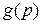 буде функція від
буде функція від 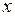 , яка дорівнює
, яка дорівнює 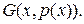
 Доведемо, що
Доведемо, що 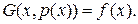 З цього приводу відмітимо, що
З цього приводу відмітимо, що 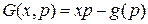 має просте геометричне розуміння: це координата дотичної до графіка
має просте геометричне розуміння: це координата дотичної до графіка 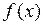 , що має нахил
, що має нахил 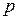 , при абсцисі
, при абсцисі 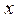 (див. рис. нижче). Дійсно, при фіксованому
(див. рис. нижче). Дійсно, при фіксованому 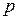 функція
функція 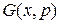 є лінійна функція від
є лінійна функція від 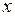 , при цьому
, при цьому 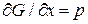 , і при
, і при 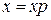 маємо
маємо 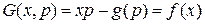 для визначення
для визначення 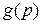 .
.
Зафіксуємо тепер 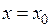 і будемо змінювати
і будемо змінювати 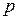 . Тоді значення
. Тоді значення 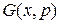 будуть ординатами точок перетину прямої
будуть ординатами точок перетину прямої 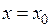 з дотичними до графіка
з дотичними до графіка 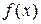 , що мають різний нахил
, що мають різний нахил 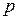 . Із опуклості графіка витікає, що всі ці дотичні лежать нижче кривої, а тому максимум
. Із опуклості графіка витікає, що всі ці дотичні лежать нижче кривої, а тому максимум 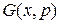 при фіксованому
при фіксованому 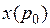 дорівнює
дорівнює 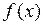 (і досягається при
(і досягається при 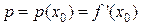 ), щ.м.б.д.
), щ.м.б.д.
Слідство.Нехай дано сімейство прямих 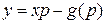 . Тоді обгинаючи має рівняння
. Тоді обгинаючи має рівняння 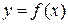 , де
, де 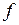 - перетворення Лежандра функції
- перетворення Лежандра функції 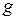 .
.
 Приклад 1
Приклад 1
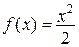 ,
, 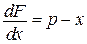 ,
, 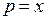 ,
, 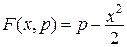 ,
,
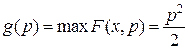 ,
, 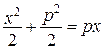 .
.
Стосовно цього прикладу зазначимо, що рівність 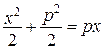 можлива лише за умови
можлива лише за умови 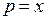 . По усіх інших значеннях
. По усіх інших значеннях 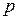 і
і 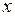 має місце нерівність Юнга
має місце нерівність Юнга 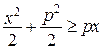 . В цьому легко пересвідчитись з рисунка. Площа трикутників
. В цьому легко пересвідчитись з рисунка. Площа трикутників
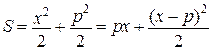
і має min при 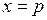 . В усіх інших випадках
. В усіх інших випадках 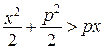 , що очевидно також, якщо записати вираз
, що очевидно також, якщо записати вираз 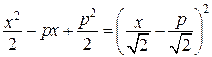 , який завжди більше або дорівнює нулеві. Причому нулю він дорівнює при
, який завжди більше або дорівнює нулеві. Причому нулю він дорівнює при 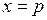 .
.
Функції 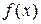 і
і 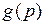 , які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом.
, які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом.
 Теорема.Значення квадратичної форми
Теорема.Значення квадратичної форми 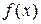 і її перетворення Лежандра
і її перетворення Лежандра 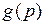 в відповідних точках співпадають:
в відповідних точках співпадають: 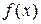 =
= 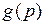 .
.
Приклад 2
Для форми 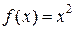 це відома властивість дотичної до параболи. Для форми
це відома властивість дотичної до параболи. Для форми 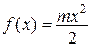 маємо
маємо 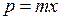 і
і 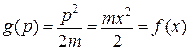 .
.
Доведення. З теореми Ейлера про однорідні функції
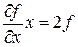 .
.
Отже, 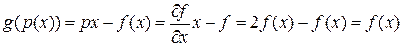 , щ.м.б.д.
, щ.м.б.д.
Випадок багатьох змінних.Нехай тепер 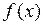 опукла функція векторного змінного
опукла функція векторного змінного 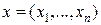 (тобто квадратична форма
(тобто квадратична форма 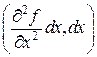 позитивно визначена). Тоді перетворення Лежандра називається функція
позитивно визначена). Тоді перетворення Лежандра називається функція 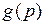 векторного змінного
векторного змінного 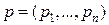 , що визначена аналогічними попередніми рівностями
, що визначена аналогічними попередніми рівностями
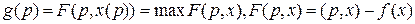 ,
,
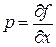 .
.
Усі попередні міркування, в тому числі нерівність Юнга, без змін переносяться на цей випадок.
Отже, функції 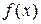 і
і 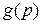 , які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом.
, які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом.
Аналогічні висновки можна зробити і при нелінійній залежності 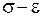 .
.
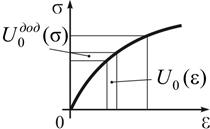 Рис. 7.5
Рис. 7.5
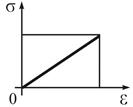 Рис. 7.6
Рис. 7.6
|   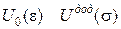
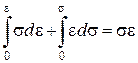 ,
де ,
де 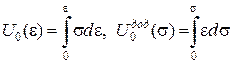 – двоїсті за Юнгом функції. – двоїсті за Юнгом функції.
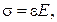
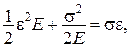
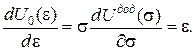
|
 Приклад 3
Приклад 3
Робота зовнішніх сил
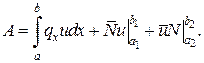
При цьому
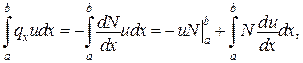
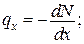
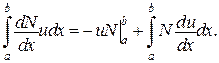
Основна інтегральна формула (формула Гріна):
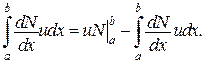
Тоді отримаємо
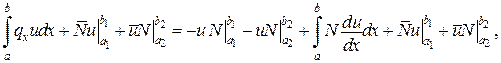
відомий вираз для теореми Клапейрона.
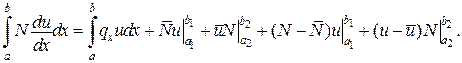
При 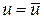 (див. рис.)
(див. рис.)
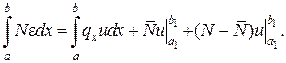
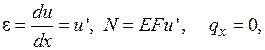
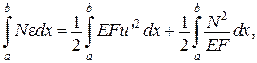
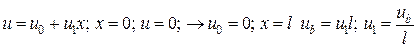
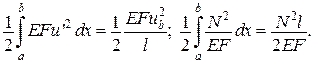
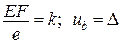
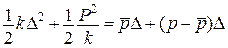
При 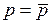

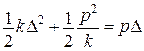

Функції потенціальної енергії пружної деформації 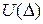 і додаткової енергії
і додаткової енергії 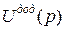 є двоїстими за Юнгом і пов’язані між собою перетворенням Лежандра. Умови екстремуму дають відповідно теореми:
є двоїстими за Юнгом і пов’язані між собою перетворенням Лежандра. Умови екстремуму дають відповідно теореми:
| Теорема Лагранжа | Теорема Кастільяно |
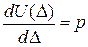
| 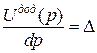
|
Перша похідна від потенціальної енергії пружної деформації по узагальненому переміщення дорівнює відповідній узагальненій силі:

| Перша похідна від додаткової потенціальної енергії по узагальненій силі дорівнює відповідному узагальненому переміщенню:
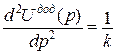
|
Другі похідні від потенціальної енергії пружної деформації по переміщенню і від додаткової потенціальної енергії по відповідній дорівнюють відповідно коефіцієнтам матриці жорсткості та матриці піддатливості.
Теорема Донкіна
Нехай задана деяка функція 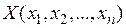 , гесіан якої відмінний від нуля:
, гесіан якої відмінний від нуля:
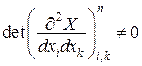 (1)
(1)
і нехай існує перетворення змінних, викликане функцією 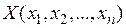 :
:
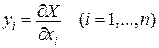 . (2)
. (2)
Тоді існує перетворення, зворотне до перетворення (2), яке теж породжено деякою функцією 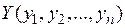 :
:
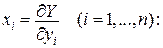 (3)
(3)
при цьому функція Y, що породжує функцію зворотного перетворення, пов’язана з функцією Х, що породжує пряме перетворення, формулою:
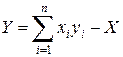 . (4)
. (4)
Якщо функція включає параметри 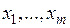 , тобто
, тобто 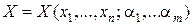 то Y теж включає ці параметри, тобто
то Y теж включає ці параметри, тобто 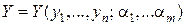 і
і
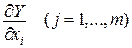 . (5)
. (5)
Доведення. Гесіан функції X співпадає з якобіаном правих частин у рівнянні (2) . Тому умова (1) показує, що з рівняння (2) показати змінні 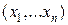 через
через 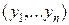 :
:
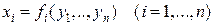 .
.
Нехай функція 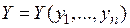 виражена формулою (4), в якій змінні
виражена формулою (4), в якій змінні 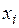 замінені виразами (15). Тоді
замінені виразами (15). Тоді
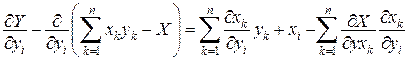 .
.
Але згідно рівняння (2), два доданки, які знаходяться в правій частині цього рівняння, взаємознищуються і отже має місце формула (3).
Нехай тепер X включає окрім змінних 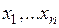 ще і параметри
ще і параметри 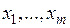 . Тоді ці параметри є в прямому перетворенні(2) , а значить і в зворотному:
. Тоді ці параметри є в прямому перетворенні(2) , а значить і в зворотному:
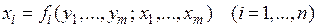 .
.
Функція Y визначається рівністю (13), де 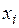 замінені на
замінені на 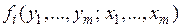 , тому
, тому

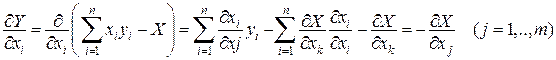 .
.
Теорема Донкіна доведена.
Приклад 4
Центральний розтяг стержня силою Р.
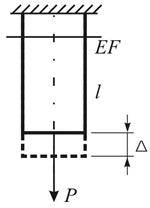
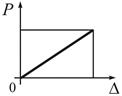 Рис. 7.8
Рис. 7.8
| 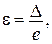 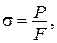
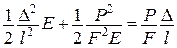
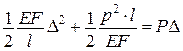 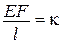
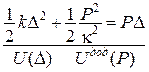 При деформації
При деформації 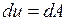 і, відповідно, і, відповідно,
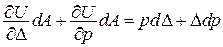 , ,
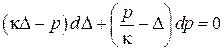
|
можна отримати рівняння рівноваги 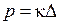 і сумісності деформацій
і сумісності деформацій 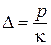 .
.
Теорема Донкіна
Якщо дві двоїстості за Юнгом функції напружень 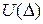 і
і 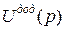 залежать від одного і того ж параметра або групи параметрів, який не є активними, тобто не приймають участі у перетворенні Лежандра (
залежать від одного і того ж параметра або групи параметрів, який не є активними, тобто не приймають участі у перетворенні Лежандра ( 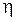 ), то має місце залежність:
), то має місце залежність:
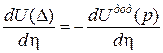
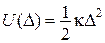
| 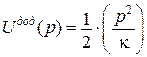
|
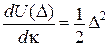
| 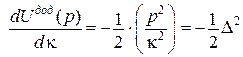
|
| У загальному випадку теореми Лагранжа і Кастільяно дають: | |
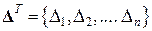
| 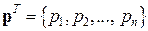
|
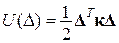
| 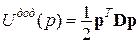
|
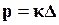
| 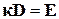 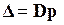
|
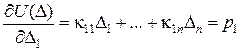
| 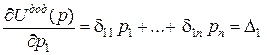
|
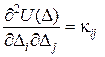
| 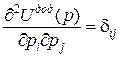
|
В будівельній механіці функції потенціальної енергії пружної деформації і додатковою потенціальної енергії є позитивно визначеними квадратичними формами. Вони є двоїстими за Юнгом функціями і пов’язані між собою перетворенням Лежандра. Перетворення Лежандра є частинним випадком нерівності Юнга-Фенхеля і за фізичним змістом являє собою рівність робіт внутрішніх і зовнішніх сил, тобто відповідає теоремі Клапейрона. Екстремуми двоїстих функцій пружної деформації і додаткової енергії дають теореми Лагранжа і Кастільяно, та призводять до систем лінійних алгебраїчних рівнянь матриці яких (матриці жорсткості і матриці піддатливості) є відповідно матрицями Гессе або матрицями других похідних відповідно від потенціальної енергії пружної деформації (матриця жорсткості) і додаткової потенціальної енергії (матриця піддатливості). Вони (матриці) є позитивно визначеними і задовольняють критеріям Сильвестра, тобто усі їх головні мінори є позитивно визначені. Вони є взаємно оберненими.
Лекція 8
Дата добавления: 2016-12-26; просмотров: 1134;
