Робота зовнішніх сил. Теорема Клапейрона. Принципи Лагранжа і Кастільяно.
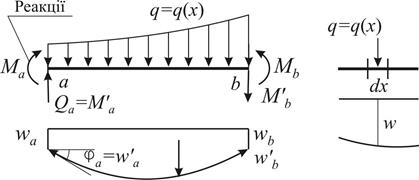
Рис. 5.1
Робота зовнішніх сил з урахуванням рівняння рівноваги 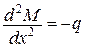 дорівнює
дорівнює
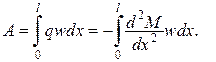
Перетворимо інтеграл у правій частині за допомогою формули інтегрування по частинах
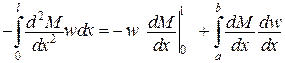 ,
,
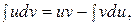
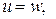
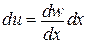 ,
,
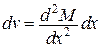 ,
, 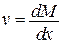 ,
,
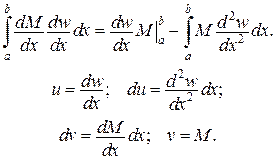
Тоді основна інтегральна формула (формула Гріна) має вигляд:
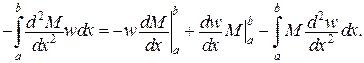
Звідси
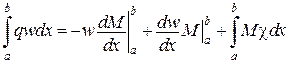 ,
,
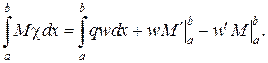
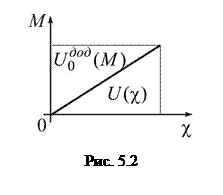
Для лінійної пружної системи (рис. 5.2)
 .
.
З урахуванням прийнятих позначень граничних умов
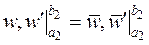 ,
, 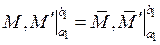 .
.
Остаточно отримаємо
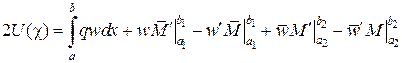 (♦)
(♦)
за умов:
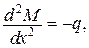
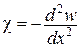 ,
, 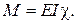
Вираз (♦) являє собою відому теорему Клапейрона: для дійсного стану лінійно пружної системи, у якому задовольняються рівняння рівноваги, сумісності деформацій, фізичної сторони задачі та граничні умови, подвійна потенціальна енергія пружної деформації доравнює роботі зовнішніх сил.
Ураховуючи, що робота внутрішніх сил ототожнюється з потенціальною енергією пружної деформації і за законом збереження енергії дорівнює роботі зовнішніх сил згідно з теоремою Клапейрона: при статичному навантаженні лінійно-пружної системи, яка знаходиться у дійсному стані, робота зовнішніх сил обчислюється як половина добутку остаточного значення узагальненої силина остаточне значення відповідного узагальненого переміщення. Якщо зовнішнє навантаження є кінематичним, тобто задається за допомогою узагальнених переміщень, то робота внутрішніх сил ототожнюється із додатковою потенціальною енергією, яка для лінійно-пружної системи дорівнює потенціальній енергії пружної деформації.
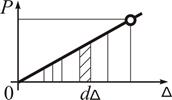 Рис. 5.3
Рис. 5.3
| 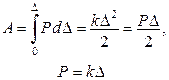
|
Принципи Лагранжа і Кастільяно
Основна інтегральна формула (формула Гріна)
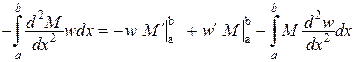
дозволяє переносити диференціальний оператор з однієї функції на іншу.
Витікає залежність, яка по суті являє собою рівність робіт внутрішніх і зовнішніх сил
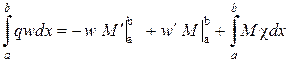
або
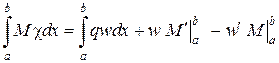 . (♦♦)
. (♦♦)
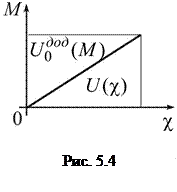
Оскільки (див. рис. 5.4)
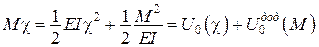
і, відповідно,
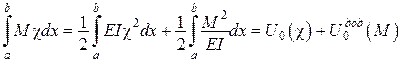 .
.
Для лінійних задач 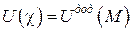 .
.
Тоді отримаємо формулу Клапейрона
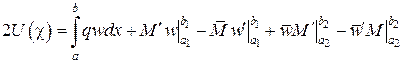 , (♦♦♦)
, (♦♦♦)
де робота зовнішніх сил на границях записана з урахуванням граничних умов
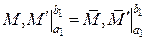 і
і 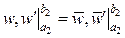 .
.
Оскільки при отриманні залежностей (♦♦), (♦♦♦) використані умови рівноваги 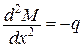 , сумісності деформацій
, сумісності деформацій 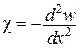 , фізичної сторони задачі
, фізичної сторони задачі 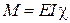 , а також наведені вище граничні умови, можна стверджувати, що функції
, а також наведені вище граничні умови, можна стверджувати, що функції 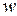 і
і 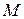 , які входять до них, є дійсними.
, які входять до них, є дійсними.
Тепер у залежності

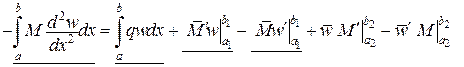 ,
,
де, відповідно, підкреслені члени, які залежать від 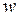 і
і 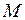 , будемо варіювати
, будемо варіювати
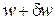 (ліворуч) (ліворуч)
| 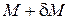 (праворуч) (праворуч)
|
Урахуємо, що

| Урахуємо, що

|
а підстановка першого члену 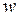 дає тотожність.
Остаточно отримаємо таке варіаційне рівняння дає тотожність.
Остаточно отримаємо таке варіаційне рівняння
| а підстановка першого члену 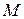 дає тотожність.
Остаточно отримаємо таке варіаційне рівняння дає тотожність.
Остаточно отримаємо таке варіаційне рівняння
|
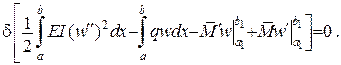
| 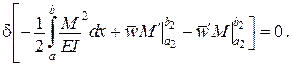
|
Воно має назву варіаційного рівняння Лагранжа
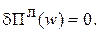
| Воно має назву варіаційного рівняння Кастільяно
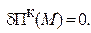
|
Відповідний функціонал має назву функціонала Лагранжа (залежить від функції 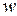 ) )
| Відповідний функціонал має назву функціонала Кастільяно[7] (залежить від функції 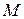 ) )
|
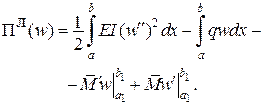
| 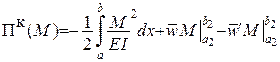 . .
|
Наведені варіаційні рівняння за змістом відображають принцип Лагранжа і принцип Кастільяно. Тобто всі 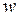 і
і 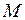 є дійсними, оскільки вони задовольняють рівнянням рівноваги, сумісності деформацій, граничним умовам.
є дійсними, оскільки вони задовольняють рівнянням рівноваги, сумісності деформацій, граничним умовам.
 Причому маємо такі додаткові умови.
1. Граничні умови:
Причому маємо такі додаткові умови.
1. Граничні умови:
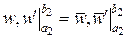 . .
|  Причому маємо такі додаткові умови.
1. Граничні умови:
Причому маємо такі додаткові умови.
1. Граничні умови:
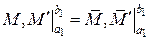
|
2. Рівняння сумісності деформацій:
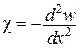 ,
а також ,
а також
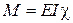 . .
| 2. Рівняння рівноваги:
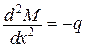 ,
а також ,
а також
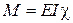 . .
|
| Принцип Лагранжа | Принцип Кастільяно |
З усіх можливих систем переміщень дійсні переміщення 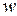 надають функціоналу Лагранжа стаціонарне (мінімальне) значення. надають функціоналу Лагранжа стаціонарне (мінімальне) значення.
| З усіх можливих систем зусиль дійсні зусилля М надають функ-ціоналу Кастільяно стаціонарне (максимальне) значення. |
| Під можливими переміщеннями розуміють переміщення, які задовольняють умовам в’язей | Під можливими зусиллями розуміють зусилля, які задоволь-няють рівнянням статики і статич- ним граничним умовам |
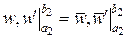
| 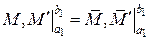
|
(кінематичним граничним умовам), а також умовам сумісності деформацій
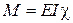 , , 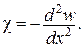
| 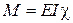 , , 
|
Оскільки функціонал Лагранжа залежить від другої похідної, маємо

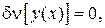
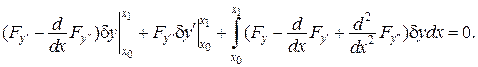
У нашому випадку
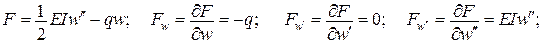
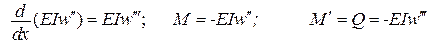
Тоді варіаційне рівняння для функціонала Лагранжа має вигляд
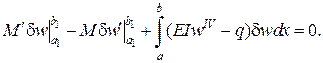
У загальному випадку при 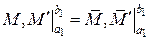 отримаємо
отримаємо
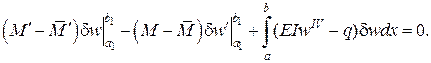
Лекція 6
Дата добавления: 2016-12-26; просмотров: 1123;
