Робота внутрішніх сил. Потенціальна енергія пружної деформації. Додаткова потенціальна енергія. Теореми Дж. Гріна і Кастільяно
Потенціальна енергія пружної деформації ототожнюється з роботою внутрішніх сил і за законом збереження енергії - відповідно з роботою зовнішніх сил.
Розглянемо нескінченно малий елемент, який знаходиться в умовах одновісного напружено-деформованого стану.
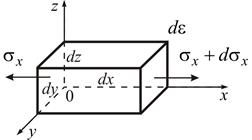 Рис. 4.1
Рис. 4.1
| Деформація 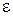 змінюється змінюється 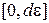 .
У загальному випадку .
У загальному випадку
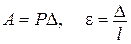 , , 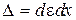 .
Робота внутрішніх сил .
Робота внутрішніх сил
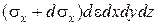 . .
|
Для одновимірної задачі надалі 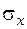 позначимо
позначимо 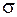
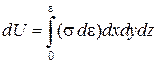 .
.
Повна потенціальна енергія тіла дорівнює:
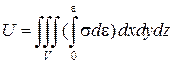 .
.
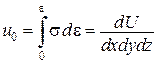 – питома (на одиницю об’єму) потенціальна енергія пружної деформації.
– питома (на одиницю об’єму) потенціальна енергія пружної деформації.
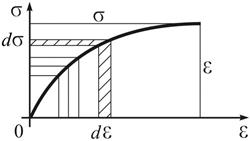 Рис. 4.2
Рис. 4.2
| 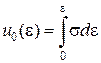 – питома потенціальна енергія пружної деформації.
Додаткова питома потенціальна енергія (термін «додаткова» пов’язується з доповненням до прямокутника) – питома потенціальна енергія пружної деформації.
Додаткова питома потенціальна енергія (термін «додаткова» пов’язується з доповненням до прямокутника)
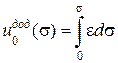 . .
|
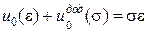 .
.
Цей вираз має назву перетворення Лежандра.
Функції, які пов’язані між собою перетворенням Лежандра, називаються двоїстими за Юнгом.
Похідні від цих функцій дорівнюють відповідно:
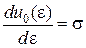 . .
| 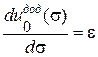 . .
|
У випадку закону Гука 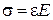 відповідно: відповідно:
| |
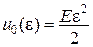 . .
| 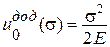 . .
|
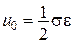 .
Перші похідні: .
Перші похідні:
| |
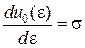 . .
| 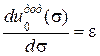 . .
|
| Ці формули мають назву: | |
| Формула Дж. Гріна | Формула Кастільяно |
| Другі похідні визначають відповідно коефіцієнти жорсткості і піддатливості: | |
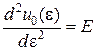 . .
| 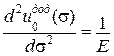 . .
|
Зазначимо, що у загальному випадку просторової задачі теорії пружності будемо мати такі залежності:
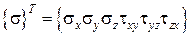 ,
,
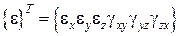 ,
,
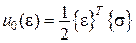 ,
,
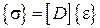 ,
, 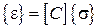 ,
,
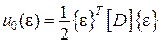 ,
,
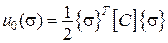 ,
,
де 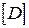 - матриця жорсткості,
- матриця жорсткості, 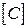 - матриця піддатливості.
- матриця піддатливості.
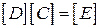 ,
,
де 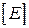 - одинична матриця.
- одинична матриця.
| Формули Дж. Гріна | Формули Кастільяно | ||
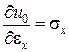
| 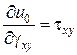
| 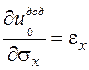
| 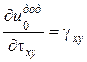
|
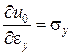
| 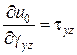
| 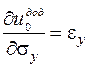
| 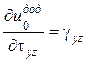
|
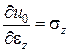
| 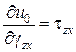
| 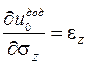
| 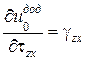
|
Потенціальна енергія згину балки з урахуванням наведених вище залежностей:
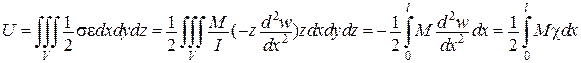 ,
,
де, відповідно
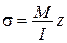 ,
, 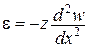 ,
, 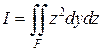 .
.
Таким чином, потенціальна енергія:
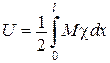
Ураховуючи, що 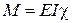 отримаємо
отримаємо
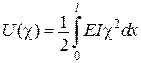
| 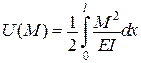
|
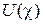 – потенціальна енергія пружної
деформації при згині балки – потенціальна енергія пружної
деформації при згині балки
| 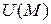 – додаткова потенціальна
енергія при згині балки – додаткова потенціальна
енергія при згині балки
|
| Питома (на одиницю довжини) потенціальна енергія пружної деформації при згині балки | Питома (на одиницю довжини) додаткова потенціальна енергія пружної деформації при згині балки | |
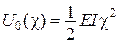
| 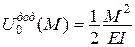
| |
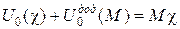 (рис. 4.3) (рис. 4.3)
| ||
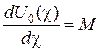
| 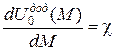
| |
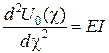
| 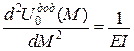
| |
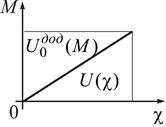 Рис. 4.3
Приклад
Рис. 4.3
Приклад
| ||
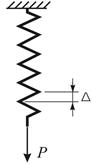 Рис. 4.4
Рис. 4.4
| 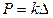 , , 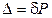 ,
де ,
де 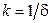 - коефіцієнт жорсткості, - коефіцієнт жорсткості, 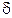 - коефіцієнт піддатливості.
Матриця Гессе (матриця других похідних). - коефіцієнт піддатливості.
Матриця Гессе (матриця других похідних).
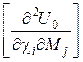
| |
Зауваження. Зазначимо, що вираз перетворення Лежандра 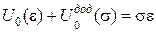 можна отримати, якщо розглядати диференціал потенціальної енергії
можна отримати, якщо розглядати диференціал потенціальної енергії 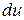 , який залежить від двох змінних -
, який залежить від двох змінних - 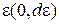 і
і 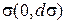 .
.
Потенціальна енергія
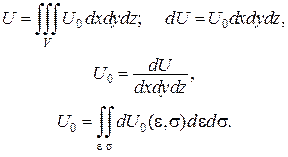
Ураховуючи, що
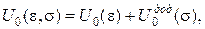
отримаємо
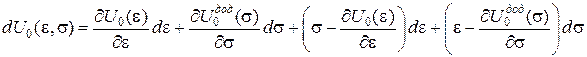
або, при 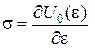 і
і 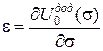 ,
,
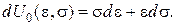
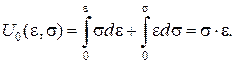
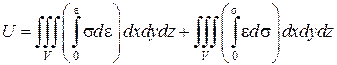 .
.
Лекція 5
Дата добавления: 2016-12-26; просмотров: 973;
