Основні поняття варіаційного числення. Функціонал і варіація. Типи задач варіаційного числення. Абсолютний і умовний екстремум. Екстремум функції і екстремум функціоналу
Функціоналами називаються змінні величини, значення яких визначаються вибором однієї або декількох функцій
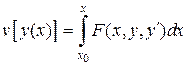 ,00
,00
де v- функціонал, y(х)- функція, F- оператор.
Приклад:
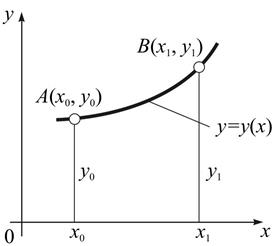 Рис. 1.1
Рис. 1.1
| Елемент довжини дуги:
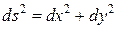 , ,
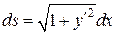 .
Довжина дуги .
Довжина дуги
 . .
|
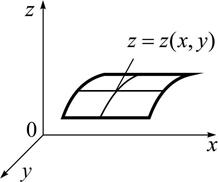 Рис. 1.2
Рис. 1.2
| Площа поверхні 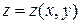
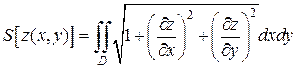 ,
де ,
де 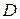 – проекція поверхні на площину – проекція поверхні на площину 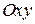 . .
|
Функціоналами є статичні моменти, координати центра ваги, моменти інерції тощо.
Функція Функціонал
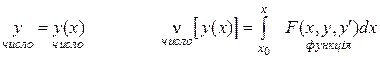 .
.
Варіаційне числення вивчає методи знаходження max, min (екстремумів) (ext), функціоналів. Задачі, які призводять до визначення ext функціоналів називаються варіаційними.
Ряд законів фізики, механіки формулюються у вигляді стверджень про те, що деякі функціонали у певному процесі досягають max або min. У такому вигляді вони мають назву варіаційних принципів. До них, зокрема, відносяться принципи збереження енергії, принципи Лагранжа, Кастільяно, Гамільтона-Остроградського, Гамільтона-Пуанкаре, Ферма та інші.
Реалізація варіаційних принципів дозволяє:
1) З’ясувати загальну енергетичну природу явищ, які вивчаються у механіці і, зокрема, у будівельній механіці;
2) Отримати автоматично рівняння рівноваги ( руху), статичні граничні умови або рівняння сумісності деформацій і кінематичні граничні умови, які інколи не можуть бути строго отримані іншими методами;
3) Отримати розв’язки задач, уникаючи процесу розв’язання диференціальних рівнянь, за допомогою так званих прямих методів варіаційного числення;
Це має принципове значення для сучасних чисельних процедур.
Характерні задачі варіаційного числення.
1) Задача про брахістохрону (лінія найшвидкого спуску)
brachistos – найкоротший, chronоs – час.
Задача поставлена у 1696 році.
Розв’язки цієї задачі були отримані: І. Бернуллі1, Я. Бернуллі 2, І. Ньютоном, Х. Гюйгенсом 3, Г.В. Лейбніцем 4, Г.Ф.А. Лопіталєм 5, Л. Ейлером, Ж. Лагранжем.

1 Бернуллі, Іоганн (нім. Johann Bernoulli, 1667—1748) — швейцарський математик, найбільш знаний представник сім’ї Бернуллі, молодший брат і учень Якоба Бернуллі, провідний математик Європи XVIII ст., вчитель Г.Ф.А.Лопіталя і Л.Ейлера. Поставив і вирішив задачу про брахістохрону, спільно з Я Бернуллі заклав основи варіаційного числення, основоположник математичної фізики. Оспорював у Якоба пріоритет у постановці варіаційної проблеми. Його наукова кореспонденція складала близько 2500 листів.
2 Бернуллі, Якоб (нім. Jakob Bernoulli, 1654—1705) — швейцарський математик, старший брат Іоганна Бернуллі. Спільно з І. Бернуллі поклав початок варіаційному численню, поставив і частково вирішив ізопериметричну задачу, а також поставлену І. Бернуллі задачу про брахістохрону, визначив форму кривої вигину пружного стрижня, ввів термін «інтеграл».
3 Гюйгенс, Християн (нідерл. Christiaan Huygens, 1629—1695) — нідерландський механік, фізик, математик, астроном і винахідник.
Задача формулюється так:
знайти форму кривої, за якої матеріальна точка (куля) скочується з точки 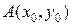 в точку
в точку 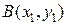 , які не лежать на одній прямій, за найкоротший час.
, які не лежать на одній прямій, за найкоротший час.
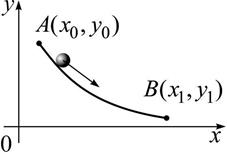 Рис. 1.3
Рис. 1.3
| 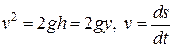 , ,
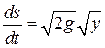 ,
де ds- елемент довжини дуги. ,
де ds- елемент довжини дуги.
|
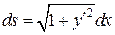 ,
,
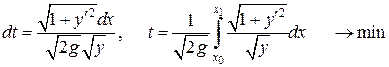 .
.
Розв’язок цієї задачі показує, що крива є циклоїдою.
Зазначимо, що у цьому випадку 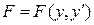 .
.

4 Лейбніц, Готфрід Вільгельм (нім. Gottfried Wilhelm von Leibniz, 1646—1716) — німецький філософ, математик, фізик, історик, юрист, дипломат, винахідник, мовознавець. Разом з І. Ньютоном поділяє заслугу заснування дифференціального і інтегрального числення.
5 Лопіталь, Гійом Франсуа Антуан (фр. Guillaume François Antoine, marquis de L'Hôpital, 1661-1704) — французський математик. У 1691-1692 рр. вивчав математику під керівництвом І.Бернуллі. Основні дослідження стосуються математичного аналізу і геометрії. Використав лекції І.Бернуллі у книзі «Аналіз нескінченно малих для дослідження кривих ліній» (1696), яка стала першим підручником з аналізу.
6 Незабаром після роботи І. Бернуллі про брахістохрону почали з'являтися (і розв’язуватися) багато задач того ж типу. І. Бернуллі поставив перед своїм учнем Л. Ейлером проблему знайти загальний підхід до їх вирішення. У 1744 р. вийшла праця Ейлера «Methodus inveniendi I lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti», «Метод знаходження кривих ліній, що мають властивості максимуму або мінімуму, або розв’язання ізопериметричної задачі, розглядуваної в найширшому сенсі», в якому були закладені теоретичні основи нового розділу математичного аналізу. Зокрема, апроксимуючи криві ламаними, Ейлер вивів диференціальне рівняння другого порядку, яке мають задовольняти екстремалі. Згодом Лагранж назвав його рівнянням Ейлера. У 1759 р. з'являється перша робота Лагранжа і з нею нові методи дослідження. Лагранж «варіює» криву, підозрювану на екстремум, виділяє з приростів функціоналів головні лінійні частини, які називає варіаціями, і користується тим, що в точці екстремуму варіація має дорівнювати нулю. Метод Лагранжа стає згодом загальноприйнятим. Цим методом і ми виведемо у подальшому рівняння Ейлера. Відзначимо, що після робіт Лагранжа за пропозицією Ейлера весь розділ математики, до якого застосовувався метод Лагранжа, почали називати варіаційним численням.
2) Задача про геодезичні лінії:
знайти лінію, яка визначає найкоротшу відстань між двома точками на поверхні.
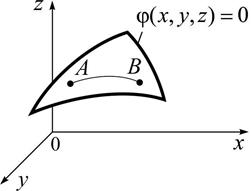 Рис. 1.4
Рис. 1.4
| 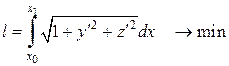 ,
де ,
де 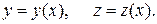 При цьому повинна бути виконана умова про те, що лінія лежить на поверхні
При цьому повинна бути виконана умова про те, що лінія лежить на поверхні  . .
|
Ця задача була розв’язана Я.Бернуллі в 1698 р., але загальний метод розв’язку таких задач був наданий лише у роботах Л.Ейлера і Ж.Лагранжа.
Такі задачі мають назву – задачі на умовний (зв’язаний) екстремум.
3) Ізопериметричні задачі. Задача Дідони.
Найдавнішою з відомих екстремальних задач є, мабуть, класична ізопериметрична задача: необхідно знайти замкнену лінію заданої довжини  , що обмежує максимальну площу
, що обмежує максимальну площу  .
.
Розв’язання ізопериметричної задачі даеться таким твердженням: якщо спрямлювана крива довжини  обмежує плоску фігуру, що має площу S, то
обмежує плоску фігуру, що має площу S, то
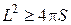 ,
,
причому рівність має місце тоді і тільки тоді, коли крива – коло.
Наведена вище нерівність називається ізопериметричною, її доведення можна знайти в [27][1].
Перша задача Дідони[2]. Серед всіх дуг довжини L, що містяться в півплощині, обмеженій прямою  , з кінцями
, з кінцями 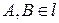 , знайти таку, яка разом з відрізком
, знайти таку, яка разом з відрізком 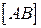 обмежує фігуру найбільшої площі S.
обмежує фігуру найбільшої площі S.
Розв’язок.
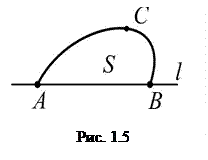 Максимальним значенням S є
Максимальним значенням S є 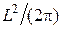 і це значення досягається, якщо
і це значення досягається, якщо 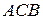 – півколо, що спирається на діаметр
– півколо, що спирається на діаметр 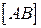 . Задача має єдиний розв’язок з точністю до зсуву вздовж прямої (рис. 1.5).
. Задача має єдиний розв’язок з точністю до зсуву вздовж прямої (рис. 1.5).
У наведеній задачі кінці А і В шуканої дуги можна вибирати на прямій  довільно. Розглянемо випадок, коли кінці дуги задаються.
довільно. Розглянемо випадок, коли кінці дуги задаються.
 Друга задача Дідони. Серед всіх дуг довжини
Друга задача Дідони. Серед всіх дуг довжини 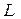 , що знаходяться в півплощині, обмеженій прямою
, що знаходяться в півплощині, обмеженій прямою  , із заданими кінцями
, із заданими кінцями 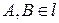 знайти таку, яка разом з відрізком
знайти таку, яка разом з відрізком 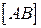 обмежує фігуру найбільшої площі.
обмежує фігуру найбільшої площі.
Розв’язок.
Як і в (1.1), рівність, а отже й максимальна площа S досягаються тоді і тільки тоді, коли крива ACBD є колом, тобто коли дуги рівні: 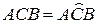 (рис. 1.6).
(рис. 1.6).
Відзначимо таку відмінність двох наведених задач. У першій задачі Дідони множина конкуруючих кривих більша, оскільки положення точок А і В не задане. Втім, не обмежуючи загальності, одну з них, скажімо А, можна вважати фіксованою. Тоді положення точки В визначається додатковою умовою:  не просто дуга кола, як у другій задачі Дідони, але
не просто дуга кола, як у другій задачі Дідони, але  є півколом, що еквівалентно твердженню: у своїх кінцях шукана дуга підходить до прямої
є півколом, що еквівалентно твердженню: у своїх кінцях шукана дуга підходить до прямої 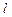 під кутом 90°. Тут проявляється загальний принцип: надаючи кінцям шуканої кривої деяку свободу, треба вимагати, щоб в них задовольнялися певні умови, які називаються умовами трансверсальності. Форма ж шуканої кривої в обох задачах однакова, вона визначається деяким рівнянням (рівнянням Ейлера), якемає задовольняти крива. У нашому випадку шукана крива в усіх точках повинна мати однакову кривизну.
під кутом 90°. Тут проявляється загальний принцип: надаючи кінцям шуканої кривої деяку свободу, треба вимагати, щоб в них задовольнялися певні умови, які називаються умовами трансверсальності. Форма ж шуканої кривої в обох задачах однакова, вона визначається деяким рівнянням (рівнянням Ейлера), якемає задовольняти крива. У нашому випадку шукана крива в усіх точках повинна мати однакову кривизну.
Ізопериметрична задача зводиться до знаходження екстремуму функціонала 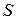 за наявності додаткової умови − довжина кривої має бути сталою, тобто значення функціонала
за наявності додаткової умови − довжина кривої має бути сталою, тобто значення функціонала
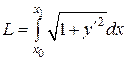 ,
,
залишається сталим. Умови такого типу називаються ізопериметричними.
У всіх наведених задачах розглядаються функціонали виду 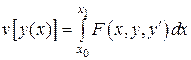 . Такі функціонали мають властивість локальності: якщо розбити криву
. Такі функціонали мають властивість локальності: якщо розбити криву 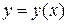 на частини і обчислити значення функціонала для кожної з них, то сума отриманих значень дорівнюватиме значенню функціонала для всієї кривої
на частини і обчислити значення функціонала для кожної з них, то сума отриманих значень дорівнюватиме значенню функціонала для всієї кривої 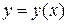 . Саме такі функціонали розглядаються у варіаційному численні.
. Саме такі функціонали розглядаються у варіаційному численні.
Деякі аналогії між математичним аналізом і варіаційним численням:
| Математичний аналіз | Варіаційне числення | ||||
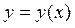
| функція | 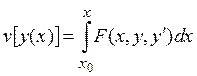
| функціонал | ||
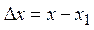
| приріст аргументу | 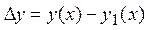
| приріст функції | ||
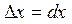
| диференціал аргументу | 
| варіація функції | ||
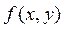
| 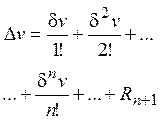
| ||||
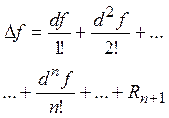
| приріст функції | приріст функціоналу | |||
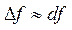
| диференціал функції | 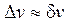
| варіація функціоналу | ||
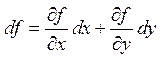
| перший диференціал функції | 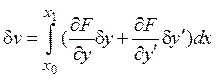
| перший диференціал функціоналу | ||
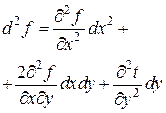
| другий диференціал функції |  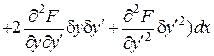
| другий диференціал функціоналу | ||
Теорема.[3] Якщо диференційована функція y=y(x) досягає max або min в будь-якій точці х=х0 області визначення, то в цій точці її перший диференціал дорівнює 0.
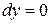
| Теорема. Якщо функціонал 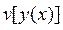 має безперервну першу варіацію і досягає max або min на будь-якій кривій, на якій він визначений, то для цієї кривої перша варіація дорівнює 0. Такі криві мають назву екстремалі. має безперервну першу варіацію і досягає max або min на будь-якій кривій, на якій він визначений, то для цієї кривої перша варіація дорівнює 0. Такі криві мають назву екстремалі.
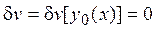
|
Схема дослідження на екстремум
| Функція | Функціонал | |||
| 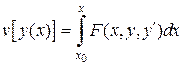
| |||
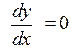 
| 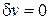 
| |||
Розв’язок рівняння 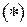 дає дає
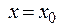
| Розв’язок рівняння 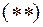 дає дає

| |||
Якщо

| 
| Якщо
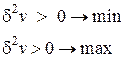
| ||
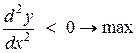
| 
| |||
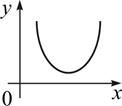
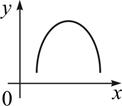
Екстремум функції
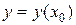 . .
| Екстремум функціоналу
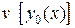 . .
|
Лекція 2(2 пари)
Дата добавления: 2016-12-26; просмотров: 2706;
