Рівняння Ейлера1 варіаційної задачі. Рівняння Ейлера-Пуассона. Приклади.
Необхідна умова екстремуму функціонала 
 ,
,
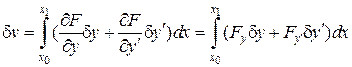 .
.
Позначимо далі

Пертворимо другий інтеграл за формулою інтегрування по частинах:
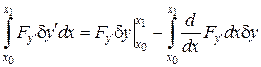 ,
,
 ,
,
 ,
, 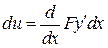 ,
,
 ,
,  ,
, 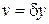 ,
,
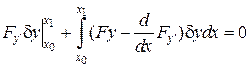 .
.
Розглянемо задачу з так званими нерухомими границями 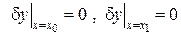 .
.

1 Ейлер, Леонард (нім. Leonhard Euler, 1707—1783) – математик, механік, фізик і астроном. Один із фундаторів варіаційного числення (праці 1727-1741 р.р.). У 1744 р. вийшла його праця «Метод нахождения кривых линий» – перша книга з варіаційного числення. Написав видатні мемуари майже по усіх галузях математики і механіки. Список його праць нараховує 850 назв, серед яких ряд багатотомних монографій. З 1909 р. у Швейцарії видається повне зібрання його творів, розраховане на 72 томи. Крім того, лише частково опублікована його наукова переписка, що охоплює 3000 листів.
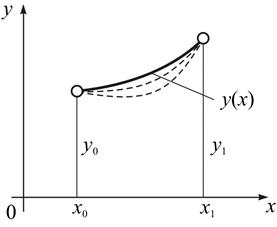 Рис. 2.1
Рис. 2.1
| Тоді отримаємо
 . .
|
Основна лема варіаційного числення ‑ лема Лагранжа[4]
Якщо функція 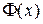 неперервна на відрізку
неперервна на відрізку 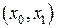 і
і

для довільної функції 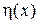 такої, що має неперервну похідну на
такої, що має неперервну похідну на 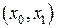 і дорівнює нулю на кінцях відрізка
і дорівнює нулю на кінцях відрізка 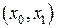 , то
, то  на відрізку
на відрізку 
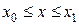 .
.
З урахуванням цієї леми отримаємо диференціальне рівняння Ейлера:
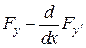 .
.
Граничні умови:
 ,
, 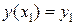 .
.
У варіаційному численні використовується ще одна лема – лема Дю-Буа-Реймонда[5].
Якщо функція 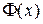 неперервна на відрізку
неперервна на відрізку 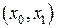 і
і
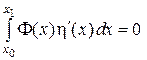
для довільної неперервної функції 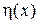 , такої що має неперервну похідну на
, такої що має неперервну похідну на 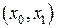 і дорівнює нулю на кінцях відрізка
і дорівнює нулю на кінцях відрізка 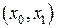 , то
, то 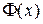 є сталою на відрізку
є сталою на відрізку 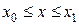 .
.
Якщо для будь-якої безперервної функції 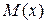 існує безперервна функція
існує безперервна функція 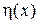 , яка має безперервну похідну
, яка має безперервну похідну  і має місце
і має місце  , то
, то  на всьому відрізку [a,b].
на всьому відрізку [a,b].
Рівняння Ейлера може бути розгорнено, якщо від функції 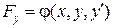 взяти похідну по х:
взяти похідну по х:
 .
.
Таким чином, отримаємо розгорнутий вираз рівняння Ейлера
 .
.
Приклад 1
Знайти екстремум функціонала довжини дуги
 , ,
 , ,
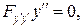
| 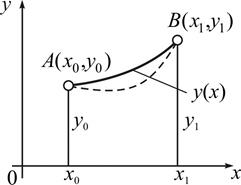 Рис. 2.2
Рис. 2.2
|


Тобто екстремалями є прямі лінії, які визначають найкоротшу відстань між точками  і
і  .
.
Приклад 2
Знайти екстремум функціонала
 .
.
Граничні умови
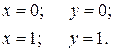
Рівняння Ейлера

 Рис. 2.3
Рис. 2.3
| Реалізація граничних умов
 дає розвязок:
дає розвязок: 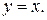
|
Таким чином екстремум функціоналу досягається на прямій 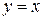 . Причому
. Причому 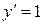 на всьому відрізку [0,1].
на всьому відрізку [0,1].
Приклад 3
Задача про брахістохрону: визначити криву, що з’єднує задані точки А і В, по якій матеріальна точка переміститься із А у В за найкоротший час (тертям і опором середовища нехтуємо).
Розмістимо початок координат в точці А, вісь  спрямуємо горизонтально, вісь
спрямуємо горизонтально, вісь 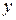 − вертикально донизу. Швидкість руху матеріальної точки
− вертикально донизу. Швидкість руху матеріальної точки  . Час, що витрачається на переміщення точки з положення
. Час, що витрачається на переміщення точки з положення 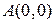 в положення
в положення 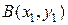 , визначається за формулою
, визначається за формулою
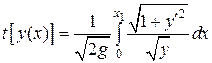 ,
,  ,
,  .
.
Оскільки цей функціонал належить до найпростішого виду і його підінтегральна функція не містить явно  , то рівняння Ейлера має перший інтеграл
, то рівняння Ейлера має перший інтеграл 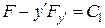 , або в даному випадку
, або в даному випадку
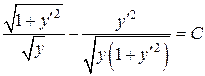 .
.
Після спрощень матимемо  або
або  . Введемо параметр
. Введемо параметр  , вважаючи
, вважаючи  , і дістанемо
, і дістанемо
 ;
;
 ;
;
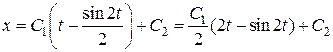 .
.
Отже, в параметричній формі рівняння шуканої лінії має вигляд
 ,
,  .
.
Змінюючи параметр за допомогою підстановки  і враховуючи, що
і враховуючи, що  , оскільки при
, оскільки при  маємо
маємо 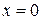 , дістанемо рівняння сімейства циклоїд у звичайній формі:
, дістанемо рівняння сімейства циклоїд у звичайній формі:
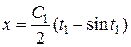 ,
,  ,
,
де  − радіус круга, що котиться. Радіус визначається з умови проходження циклоїди через точку
− радіус круга, що котиться. Радіус визначається з умови проходження циклоїди через точку 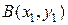 . Отже, брахістохроною є циклоїда.
. Отже, брахістохроною є циклоїда.
Функціонали, які залежать від другої похідної. Рівняння Ейлера-Пуассона[6]
Функціонал
 .
.
Варіаційне рівняння для цього функціонала має вигляд:
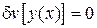 ,
,
або
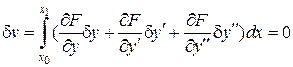 .
.
З урахуванням позначень частинних похідних

отримаємо
 .
.
До другого і третього членів цього рівняння застосуємо процедуру перетворення по частинах
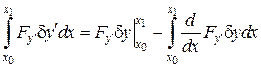 ,
,
 ,
,


 ,
,  ,
, 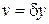 .
.
Аналогічно
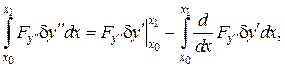

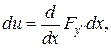

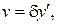


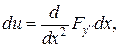


Підсумовуючи підкреслені члени отримаємо:
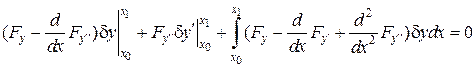 .
.
Згідно з лемою Лежандра отримаємо

– рівняння Ейлера-Пуассона для функціоналу, який залежить від другої похідної.
Граничні умови
 ,
,  ,
,
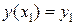 ,
,  .
.
По аналогії запишемо рівняння Ейлера-Пуассона для функціоналу, який залежить від n-ї похідної
 .
.
Рівняння Ейлера-Пуассона мають порядок 2n.
 .
.
Граничні умови
 , ,
| 
| 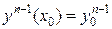
|
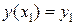
| 
| 
|
Приклад 4
 .
.
Граничні умови
 , ,
|  , ,
|
 , ,
|  . .
|
Рівняння Ейлера-Пуассона
 ,
,
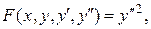

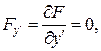

Диференціальне рівняння Ейлера 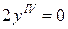 є рівняння 4 порядку.
є рівняння 4 порядку.
Загальний розв’язок:
 ,
,
 .
.
Реалізуємо граничні умови
1) 
 ,
,
2) 
 ,
,
3) 

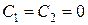 ,
,
4) 

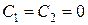 .
.
Екстремаль  .
Тобто функціонал досягає екстремуму на прямій .
Тобто функціонал досягає екстремуму на прямій 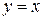 . Причому . Причому 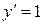 , а , а  на всьому відрізку [0,1] (див. рис.). на всьому відрізку [0,1] (див. рис.).
|  Рис. 2.4
Рис. 2.4
|
| Приклад 5 Граничні умови |  Рис. 2.5
Рис. 2.5
|

| 
|

| 
|
Тоді  .
Екстремаль .
Екстремаль 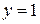 . Причому . Причому  , ,  на всьому відрізку [0,1]. на всьому відрізку [0,1].
|
Приклад 6
| Граничні умови |  Рис. 2.6
Рис. 2.6
| |||||||||||||

| 
| |||||||||||||

| 
| |||||||||||||
Тоді  , ,
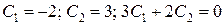 .
Екстремаль .
Екстремаль
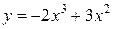 , ,
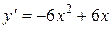 , ,
 ,
Точка перетину ,
Точка перетину
 ; ; 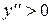 , ,
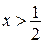 ; ;  (див. рис.). (див. рис.).
| ||||||||||||||
| Приклад 7 Граничні умови | 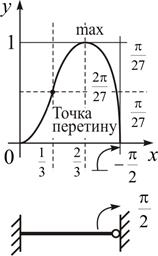 Рис. 2.7
Рис. 2.7
| |||||||||||||

| 
| |||||||||||||
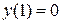
| 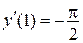
| |||||||||||||
Тоді  . .
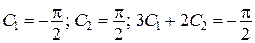 Екстремаль
Екстремаль
 , ,
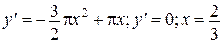 (екстремум), (екстремум),
 (точка перетину).
Точка перетину (точка перетину).
Точка перетину
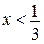 ; ; 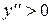
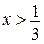 ; ;  (див. рис.). (див. рис.).
| ||||||||||||||
Екстремум при Точка перетину
| ||||||||||||||
Надалі буде показано, що вихідний функціонал  =0 являє собою функціонал Лагранжа для балки з відповідними кінематичними граничними умовами (приклади 4–9) і реалізація принципу Лагранжа призводить до відповідного рівняння Ейлера, розв’язок якого визначає лінію прогину балки.
=0 являє собою функціонал Лагранжа для балки з відповідними кінематичними граничними умовами (приклади 4–9) і реалізація принципу Лагранжа призводить до відповідного рівняння Ейлера, розв’язок якого визначає лінію прогину балки.
Лекція 3
Дата добавления: 2016-12-26; просмотров: 1997;

 Рис. 2.8
Рис. 2.8

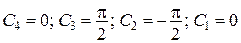 .
Екстремаль
.
Екстремаль
 ,
,
 .
Екстремум при
.
Екстремум при 

 .
.
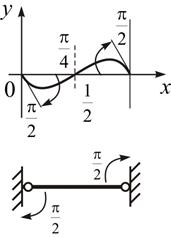 Рис. 2.9
Рис. 2.9
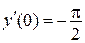
 .
Екстремаль
.
Екстремаль
 ;
;  .
.
 ;
; 
