V.1. Задача Коші для рівняння коливань струни.
РІВНЯННЯ ГІПЕРБОЛІЧНОГО ТИПУ.
Всі фізичні процеси, що пов’язані з процесами коливань, а саме – коливання струни, мембрани, газу, електромагнітні коливання, що приводять до задач, де використовуються рівняння гіперболічного типу. Характерною особливістю всіх перерахованих вище процесів є скінчена швидкість їх розповсюдження.
V.1. Задача Коші для рівняння коливань струни.
Типовий представник рівнянь цього типу - це хвильове рівняння
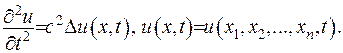 (V.1)
(V.1)
У випадку, коли 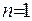 , хвильове рівняння перетворюється на рівняння коливань струни
, хвильове рівняння перетворюється на рівняння коливань струни
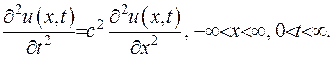 (V.2)
(V.2)
Введемо нові змінні 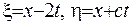 :
:
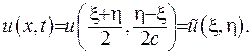 (V.3)
(V.3)
В нових змінних рівняння (V.2) прийме вигляд (див. додаток А):
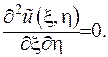 (V.4)
(V.4)
Проінтегруємо за змінною 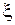 рівняння (V.4):
рівняння (V.4):
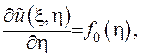
а після цього за змінною 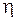 . Загальний розв’язок рівняння (V.4) отримаєно у вигляді:
. Загальний розв’язок рівняння (V.4) отримаєно у вигляді:
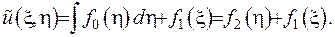
Повернувшись до вихідних змінних, запишемо розв’язок:
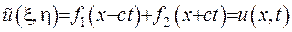 , (V.5)
, (V.5)
або 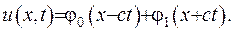
Проаналізуємо функції 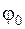 та
та 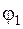 :
:
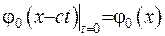 (V.6)
(V.6)
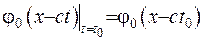 (V.7)
(V.7)
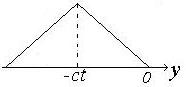
Якщо побудувати графік функції 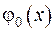 , то, як бачимо, графік функції
, то, як бачимо, графік функції 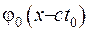 буде усунуто. Величина
буде усунуто. Величина 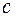 - це швидкість хвилі, а функцію
- це швидкість хвилі, а функцію 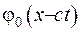 називають прямою хвилею, на відміну від
називають прямою хвилею, на відміну від 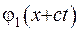 , яка є зворотнею хвилею.
, яка є зворотнею хвилею.
Їх графічне зображення дивись на рисунках.
Позначимо 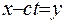 .
. 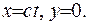
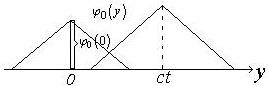
Позначимо 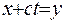 .
.
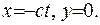
Задача Коші для рівняння коливань струни.
Розглянемо задачу
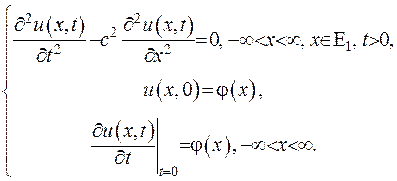 (V.8)
(V.8)
Вперше задачу (V.8) було розв’язано Даламбером. Побудуємо розв’язок та водночас встановимо, які обмеження потрібно накласти для його отримання.
Як показано раніше, розв’язок рівняння з (V.8) описується формулою (V.5). Задовольнимо першу початкову умову з (V.8):
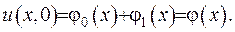 (V.9)
(V.9)
Відшукаємо похідну за часом з метою задовольнити другу початкову умову:
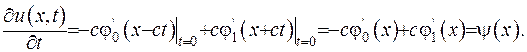 (V.10)
(V.10)
Проінтегруємо за змінною 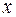 обидві частини останньої рівності:
обидві частини останньої рівності:
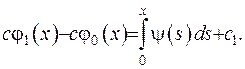 (V.11)
(V.11)
З співвідношень (V.9) та (V.11) розшукаємо 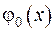 та
та 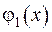 :
:
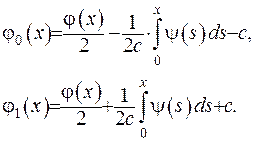 (V.12)
(V.12)
Отже, відповідно до формули (V.9) отримаємо розв’язок задачі Коші (V.8) у вигляді:
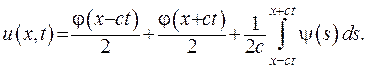 (V.13)
(V.13)
Формулу (V.13) називають формулою Даламбера, вона і є розв’язком задачі Коші для коливань струни.
Доведемо тепер, що задача Коші (V.8) має єдиний розв’язок.
Теорема. Задача Коші (V.8) має єдиний розв’язок.
Доведення. Проводитиметься від протилежного. Припустимо, що у задачі (V.8) існує два розв’язки 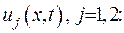
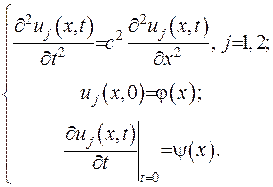 (V.14)
(V.14)
Введемо нову функцію за формулою
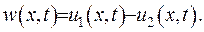 (V.15)
(V.15)
Як бачимо, вона задовольняє наступній задачі:
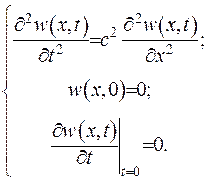 (V.16)
(V.16)
Отримано однорідну задачу з однорідними умовами. Виходячи з цього, маємо, що 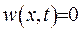 , а звідки
, а звідки 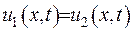 . Доведено, що задача Коші має єдиний розв’язок.
. Доведено, що задача Коші має єдиний розв’язок.
Доведемо тепер стійкість розв’язку задачі Коші для рівняння коливань струни.
Теорема. Малим змінам заданих функцій у задачі Коші для коливань струни відповідає мала зміна шуканого розв’язку.
Доведення.
Припустимо, що існує два розв’язки задачі Коші, які задовольняють відповідним початковим умовам:
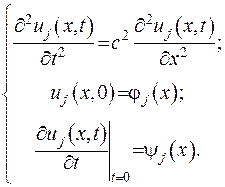 (V.17)
(V.17)
Покажемо, що якщо 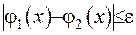 та
та 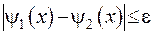 , то з цього випливає, що
, то з цього випливає, що 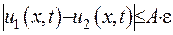 , де
, де 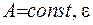 - як завгодно мале додатне число. Відповідно до формули Даламбера маємо:
- як завгодно мале додатне число. Відповідно до формули Даламбера маємо:
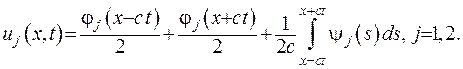
Розглянемо різницю 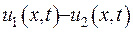 :
:
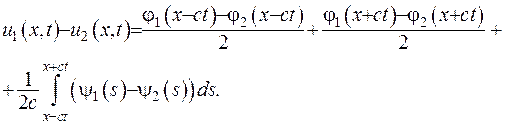 (V.18)
(V.18)
Проведемо оцінку різниці функцій за формулою (V.18):
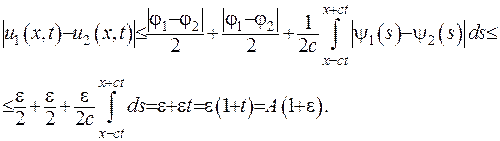
Якщо розглядувати скінчений часовій проміжок, то розв’язок задачі Коші буде стійкий.
Висновок, який можна зробити: задача Коші для рівняння коливань струни є коректно поставленою задачею математичної фізики.
Цікаво встановити, коли є справедливою формула Даламбера. Як легко перевірити, це буде, якщо 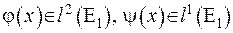 . Тобто, мають місце досить жорсткі обмеження. Для того, щоб їх трохи послабити, розглянемо замість
. Тобто, мають місце досить жорсткі обмеження. Для того, щоб їх трохи послабити, розглянемо замість 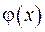 послідовність
послідовність 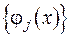 таку, що
таку, що 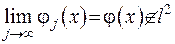 , але
, але 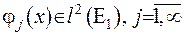 .
.
Розв’язок задачі Коші у цьому випадку будується для кожної функції 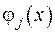 . Якщо існує межа отриманої послідовності розв’язків
. Якщо існує межа отриманої послідовності розв’язків
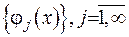 , то цю межу називають узагальненим розв’язком гіперболічного типу:
, то цю межу називають узагальненим розв’язком гіперболічного типу: 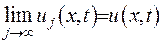 .
.
Тривимірний випадок.
Розв’яжемо частковий випадок задачі Коші для простору 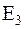 :
: 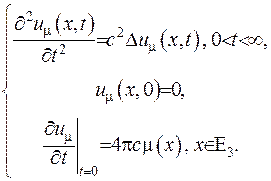 (V.19)
(V.19)
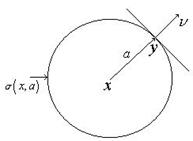
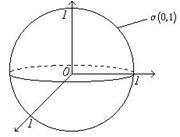
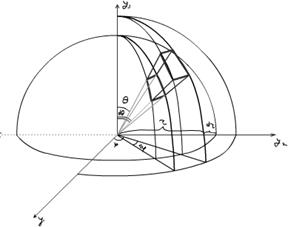
Припустимо, що 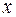 є початок сферичної системи координат і водночас центр кулі радіуса
є початок сферичної системи координат і водночас центр кулі радіуса 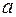 (див. рис. )
(див. рис. ) 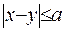 .
.
 Розв’язок поставленої задачі записується за формулою:
Розв’язок поставленої задачі записується за формулою:
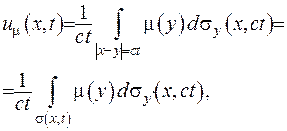 (V.20)
(V.20)
де 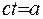 , а інтегрування проводиться за змінною
, а інтегрування проводиться за змінною 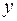 .
.
Доведемо це. З метою полекшення інтегрування за координатою, зробимо заміну змінних
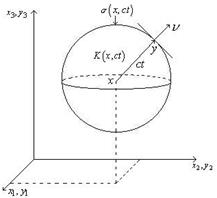
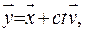 (V.21)
(V.21)
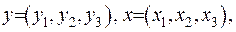
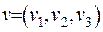 - вектори.
- вектори.
Проекції цих векторів запишемо
у вигляді: 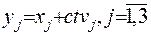 . Отже, маємо, що
. Отже, маємо, що 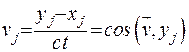 .
.
Із співвідношення (V.21) випливає, що 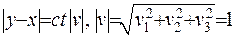 , як сума квадратів направляючих косинусів.
, як сума квадратів направляючих косинусів.
Графічно це визначає, що заміна змінних (V.21) перетворює сферу 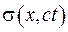 до одиничної сфери
до одиничної сфери 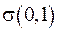 .
.
 З’ясуємо значення величини
З’ясуємо значення величини 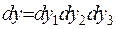 - величини об’єму елементарного паралелепіпеду – у сферичній системи координат (див.рис. ). Елемент сферичної системи
- величини об’єму елементарного паралелепіпеду – у сферичній системи координат (див.рис. ). Елемент сферичної системи 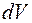 дорівнюватиме:
дорівнюватиме: 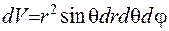 .
.
 При збільшенні радіуса сфери на величину
При збільшенні радіуса сфери на величину 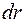 замість елемента кулі
замість елемента кулі 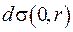 отримаємо елемент кулі
отримаємо елемент кулі 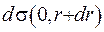 . Отже,
. Отже, 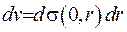 .
.
У випадку, коли радіус сфери 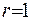
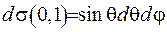 .
.
З урахуванням заміни змінних (V.21) та вищезаписаного маємо
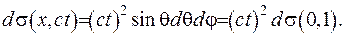 (V.22)
(V.22)
Підставимо співвідношення (V.22) до формули (V.20):
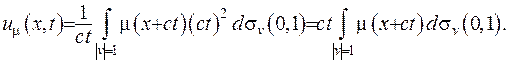 (V.23)
(V.23)
Тут точка 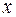 не належить області інтегрування, тому якщо
не належить області інтегрування, тому якщо 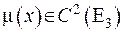 , можна застосувати до функції (V.23) оператор Лапласа:
, можна застосувати до функції (V.23) оператор Лапласа:
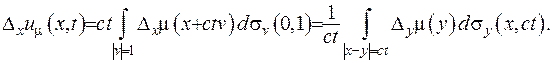 (V.24)
(V.24)
Перевіримо виконання початкових умов задачі Коші (V.19). З цією метою продиференціюємо спочатку функцію (V.23):
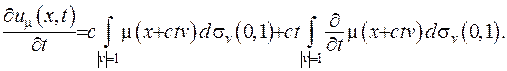 (V.25)
(V.25)
Враховуючи формулу зв’язку проекцій 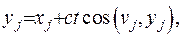 можна записати похідну за змінною
можна записати похідну за змінною 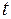 у вигляді:
у вигляді:
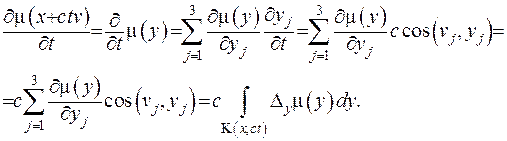
Відповідно до цього формулу (V.25) перепишемо:
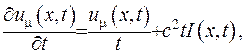 (V.26)
(V.26)
де 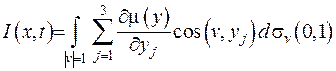 .
.
Першу початкову умову за рахунок зображення (V.23) виконано:
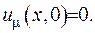
Перевіримо виконання другої початкової умови:
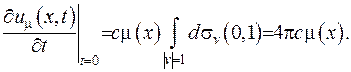
Таким чином, доведено виконання початкових умов у разі зображення розв’язку задачі Коші у вигляді (V.23). Залишилося довести, що ця функція задовольняє хвильове рівняння.
У формулі (V.26) повернемося до старих змінних:
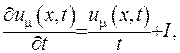 (V.27)
(V.27)
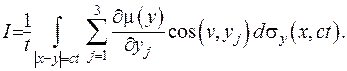
Застосуємо формулу Остроградського для випадку кулі 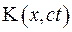 :
:
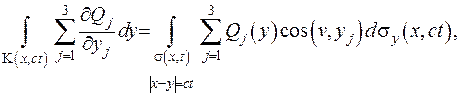 (V.28)
(V.28)
де 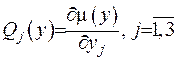 .
.
З цього випливає, що інтеграл (V.27) набуває вигляду об’ємного інтегралу:
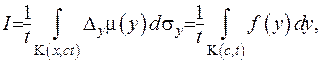 (V.29)
(V.29)
де 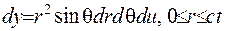 , або у іншому запису
, або у іншому запису 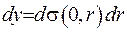 . Запишемо об’ємний інтеграл через подвійні інтеграли:
. Запишемо об’ємний інтеграл через подвійні інтеграли:
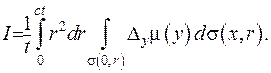 (V.30)
(V.30)
Знайдемо тепер першу та другу похідні за часом з урахуванням співвідношення (V.27) та зображення (V.30):
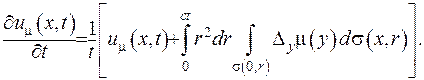 (V.31)
(V.31)
Друга похідна за часом дорівнюватиме:
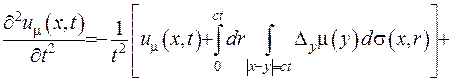
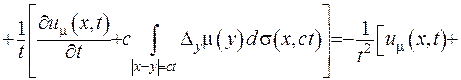
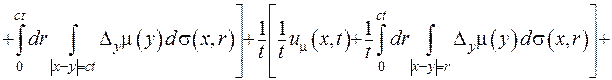
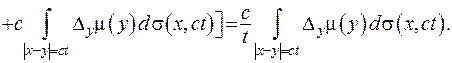 (V.32)
(V.32)
Отже, з урахуванням формул (V.24) та (V.32) доведено, що
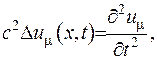
а з цього випливає, що розв’язком задачі Коші для тривимірного випадку (V.19) є зображення (V.20).
Якщо припустити, що функцію 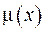 можна взяти у вигляді
можна взяти у вигляді 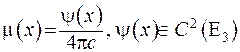 , то можна довести, що наступне зображення також задовольняє задачу Коші:
, то можна довести, що наступне зображення також задовольняє задачу Коші:
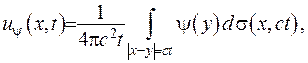 (V.33)
(V.33)
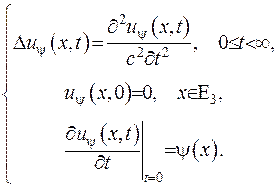
Дата добавления: 2016-05-05; просмотров: 3705;
