V.3. Формули Кірхгофа. Принцип Гюйгенса.

Розглянемо задачу Коші:

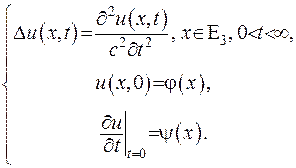(V.34)

Якщо замість невідомої функції 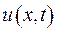ввести нову функцію 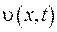за формулою

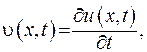(V.35)

то можна показати, що функція (V.35) задовольняє рівняння задачі:

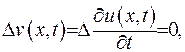
що випливає з того факту, що

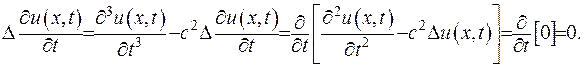
Задовольнимо початкові умови, враховуючи що

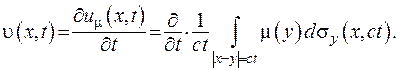(V.36)

Позначимо

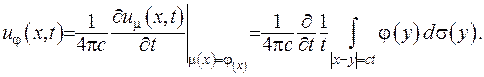
Функція (V.36) є хвильовою функцією, що задовольняє хвильове рівняння. З зображення (V.36) легко отримати, що

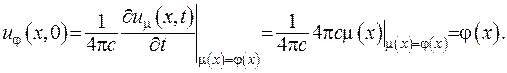
Знайдемо похідну за часом та візьмемо в неї :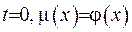

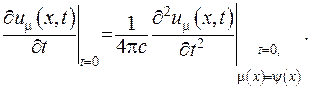
Якщо вимагати, щоби функції 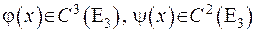, то зображення (V.36) буде задовольняти всім умовам задачі Коші, а отриману формулу називають формулою Кірхгофа:

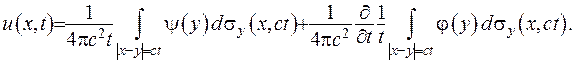(V.37)

Зформулюємо принцип Гюйгенса.

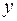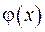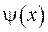Нехай у точці локалізовано вихідне збурення, тобто функції та відмінні від нуля зовні області 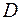. Зафіксуємо час 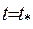, та введемо позначення: - мінімальна відстань від точки спостереження 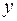до області 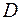, 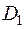- максимальна відстань. У випадку, коли 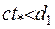, хвиля збурення ще не торкається області 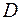на відміну від випадку 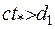, коли збурення досягли області. Аналогічним чином, якщо 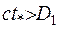, збурення пройшли область 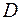та вона находиться у спокої. Таким чином, збурення будуть протікати у області 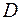, коли 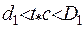. В цьому і міститься принцип Гюйгенса: локалізація у просторі початкового збурення відповідає локалізації коливань у часі.