Виведення рівняння коливань струни.

Нехай маємо струну 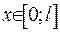, до якої додано навантаження. Передбачається, що кінці струни на нескінченності закріплені. Розглянемо ділянку струни довжиною 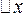. Нехай 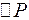- сила, що діє на цій ділянці, тоді інтенсивність навантаження у точці 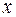визначимо за формулою

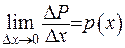. (1.26)

Припустимо, що струна 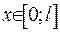завантажена рівномірно силою з інтенсивністю 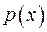. Потрібно розшукати провисання струни. У кожній точці провисання проведемо дотичну. Вважаючи, що 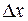- мале, можна рахувати, що функція 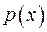є постійною, тобто 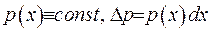. На кожну ділянку струни діють сили: 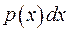та - сила натягу. Оскільки струна є у спокої, то ці сили врівноважені:

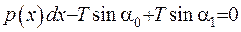. (1.27)

Тут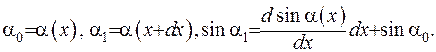

З рівняння (1.27) отримаємо умову рівноваги у вигляді

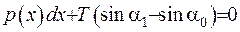
або

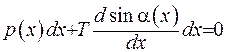(1.28)

Потрібно зауважити, що 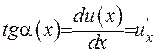, тобто 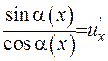. З цього випливає, що

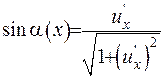. (1.29)

Якщо приймемо, що провисання мале та навантаження також невеличке, то можна вважати, що 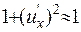. З цього маємо, що 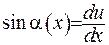. Тоді умова рівноваги (1.28) набуває вигляд:

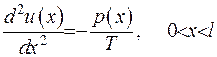(1.30)

Рівняння (1.30) є рівнянням провисання струни.

Знайдемо вигляд рівняння коливання струни. У цьому випадку всі величини залежать не тільки від координати простору, але і від часу 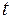.Враховуючи принцип Даламбера у рівнянні рівноваги (1.27), потрібно підключити сили інерції з протилежним знаком 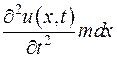, де .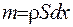

З урахуванням такого зображення інерційного члена маємо

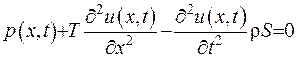
або

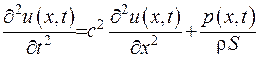, (1.31)

де введено позначення .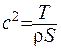

Рівняння (1.31) у випадку 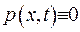є хвильовим рівнянням

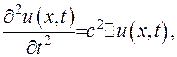
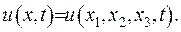(1.32)

У випадку, коли 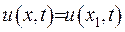, отримуємо як частковий випадок рівняння коливання для струни

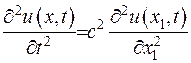(1.33)

З’ясуємо тепер, яким вимогам мають задовольняти задачі математичної фізики, та які задачі розглядатимуться у курсі.