Приклади реалізації принципів Лагранжа і Кастільяно
Розвяжемо задачу показану на рис. 8.1.
1. Функціонал Лагранжа.
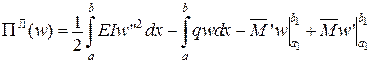 ,
,
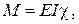
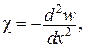
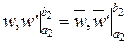 .
.
 Граничні умови задаються тільки для
Граничні умови задаються тільки для  , оскільки розглядається функціонал Лагранжа.
, оскільки розглядається функціонал Лагранжа.
Приймемо, що
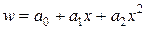 ,
,
де  - невідомі константи.
- невідомі константи.
Реалізуючи граничні умови, отримаємо:
1) 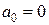 ;
;
2) 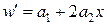 ,
, 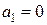 .
.
Таким чином
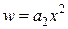 ;
; 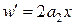 ;
; 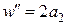 ,
,
а
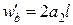 ,
, 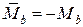 .
.
Функціонал, а після інтегрування – функція Лагранжа, має вигляд:
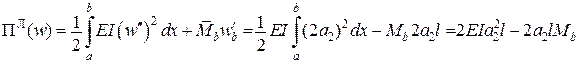 .
.
Знаходимо мінімум екстремум функції 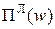

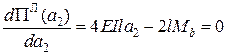 ,
,
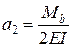 ,
, 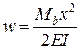 ,
,
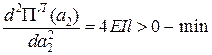 ,
,
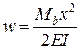 .
.
2. Функціонал Кастільяно
Розглянемо розв’язок цієї ж самої задачі за допомогою функціонала Кастільяно, який для даного випадку має вигляд

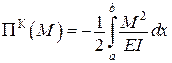 .
.
Додаткові умови:
- рівняння рівноваги
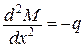 .
.
- граничні умови
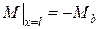 .
.
Користуючись правилом множників Лагранжа, послідовно отримаємо:
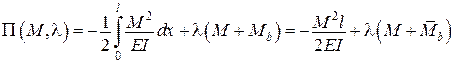 ,
,
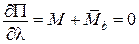 ;
; 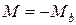 ;
;
 ;
; 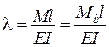 .
.
 Зазначимо, що за фізичним змістом невідомий множник Лагранжа
Зазначимо, що за фізичним змістом невідомий множник Лагранжа 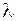 являє собою кут повороту кінця балки.
являє собою кут повороту кінця балки.
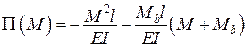 ,
,
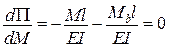 ,
, 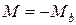 ,
,
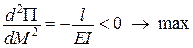 ,
,
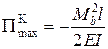 .
.
3. Функціонал Кастільяно
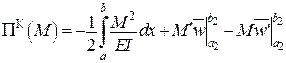 .
.
Додаткові умови
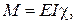
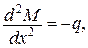
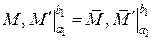 .
.
 Для даної задачі (рис. 8.5)
Для даної задачі (рис. 8.5)
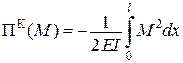 .
.
Розшукуємо 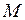 у вигляді ряду
у вигляді ряду
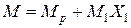 ,
,
або (див. рис. 8.5)
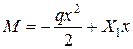 ,
,
де невідомою є 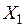 .
.
Перевіримо виконання додаткових умов
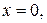
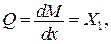
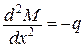
і підставимо до вихідного функціоналу
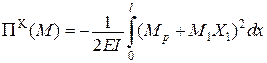 .
.
Знайдемо екстремум 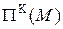
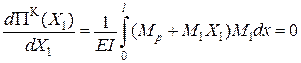 .
.
Таким чином ми отримали відповідне рівняння методу сил
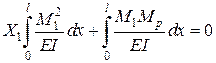 ,
, 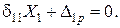
Дата добавления: 2016-12-26; просмотров: 678;
