Афінні перетворення нормально розподілених векторів
Нехай 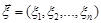 – неперервний нормально розподілений випадковий вектор, щільність розподілу якого задається формулою (19.2).
– неперервний нормально розподілений випадковий вектор, щільність розподілу якого задається формулою (19.2).
Означення 19.2. Перетворення вигляду 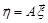 , де
, де 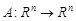 – лінійний оператор (матриця) назвемо афінним.
– лінійний оператор (матриця) назвемо афінним.
Оскільки в 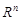 зафіксовано ортонормований базис, то А задає матрицю перетворення в цьому базисі. Розглянемо матрицю
зафіксовано ортонормований базис, то А задає матрицю перетворення в цьому базисі. Розглянемо матрицю 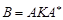 , де
, де 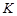 – кореляційна матриця вектора
– кореляційна матриця вектора 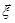 , яка має діагональний вигляд із елементами
, яка має діагональний вигляд із елементами 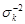 на головній діагоналі. Матриця
на головній діагоналі. Матриця 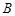 є симетрична додатна визначена матриця. Дійсно
є симетрична додатна визначена матриця. Дійсно
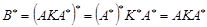 ,
,
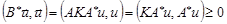 .
.
Тоді відомо, що існує ортогональна матриця 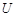 та діагональна матриця
та діагональна матриця 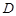 з невід’ємними діагональними елементами, така, що
з невід’ємними діагональними елементами, така, що 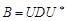 . При цьому діагональні елементи матриці
. При цьому діагональні елементи матриці 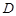 , які позначимо
, які позначимо 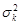 є власні числа матриці
є власні числа матриці 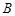 , а матриця
, а матриця 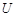 відповідає перетворенню даного базису в базис, що складається з власних векторів матриці
відповідає перетворенню даного базису в базис, що складається з власних векторів матриці 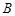 . Методом характеристичних функцій (тема 4) можна довести, що випадковий вектор
. Методом характеристичних функцій (тема 4) можна довести, що випадковий вектор 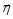 також буде нормально розподіленим з кореляційною матрицею
також буде нормально розподіленим з кореляційною матрицею 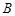 і щільністю розподілу
і щільністю розподілу
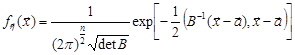 ,
,
причому 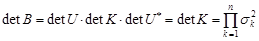 .
.
Наведемо без доведення такі властивості закону Гаусса:
1. Якщо випадковий вектор 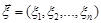 має нормальний розподіл, то “скорочений” вектор
має нормальний розподіл, то “скорочений” вектор 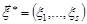 , де
, де 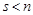 також має нормальний розподіл.
також має нормальний розподіл.
2. Якщо вектори 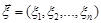 та
та 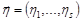 незалежні нормально розподілені вектори, то вектор
незалежні нормально розподілені вектори, то вектор 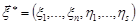 також буде нормально розподіленим вектором.
також буде нормально розподіленим вектором.
Приклад 19.3. Знайти закон розподілу компоненти 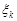 нормально розподіленого вектора
нормально розподіленого вектора 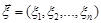 .
.
Розв’язання. Очевидно, що випадкова компонента
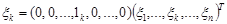 .
.
Це означає, що компоненту 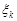 нормально розподіленого вектора
нормально розподіленого вектора 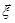 можна отримати афінним перетворенням, для якого
можна отримати афінним перетворенням, для якого 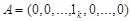 . Щільність розподілу
. Щільність розподілу 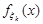 компоненти
компоненти 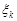 є щільність нормального розподілу з параметрами
є щільність нормального розподілу з параметрами
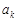 та
та 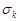 , тобто
, тобто 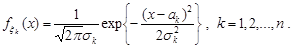
Отже, координати нормально розподіленого вектора також нормально розподілені величини. Обернене твердження, взагалі кажучи, виконується не завжди, тому що необхідне виконання умови незалежності компонент вектора.
Приклад 19.4. Знайти закон розподілу суми компонент нормально розподіленого вектора 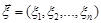 .
.
Розв’язання. Очевидно, що суму компонент випадкового вектора можна записати так:
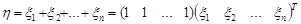 .
.
Тобто суму компонент нормально розподіленого вектора можна отримати афінним перетворенням, для якого 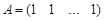 . Отже, сума компонент нормального вектора є нормально розподілена випадкова величина з параметрами
. Отже, сума компонент нормального вектора є нормально розподілена випадкова величина з параметрами
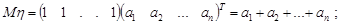
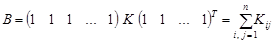 .
.
Отже, щільність розподілу 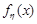 суми компонент нормального вектора має вигляд
суми компонент нормального вектора має вигляд
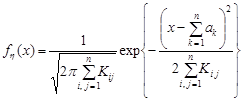 .
.
Оскільки незалежні випадкові величини 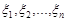 , які нормально розподілені з параметрами
, які нормально розподілені з параметрами 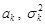 можна вважати компонентами нормального вектору, то можна стверджувати, що їх сума
можна вважати компонентами нормального вектору, то можна стверджувати, що їх сума 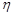 є нормально розподілена випадкова величина з параметрами
є нормально розподілена випадкова величина з параметрами
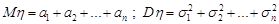 .
.
Загальне твердження, що сума нормально розподілених випадкових величин є величина, яка розподілена за законом Гаусса, взагалі кажучи, невірне.
Приклад 19.5. Нехай 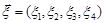 нормально розподілений випадковий вектор з параметрами
нормально розподілений випадковий вектор з параметрами 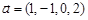 та кореляційною матрицею
та кореляційною матрицею
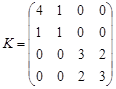 .
.
Знайти щільність розподілу цього вектора.
Розв’язання. Із вигляду кореляційної матриці робимо висновок, що вектори 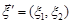 та
та 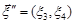 – незалежні. Тобто щільність розподілу
– незалежні. Тобто щільність розподілу 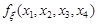 вектора
вектора 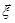 можна записати через щільність розподілу підсистем цього вектора
можна записати через щільність розподілу підсистем цього вектора  та
та 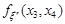
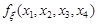 =
= 
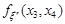 .
.
Це випливає з того, що 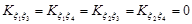 .
.
Випадкові вектори 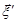 та
та 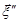 –нормально розподілені, оскільки кожен із них можна отримати афінним перетворенням із вектора
–нормально розподілені, оскільки кожен із них можна отримати афінним перетворенням із вектора 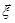 :
:
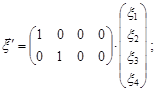
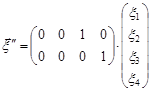 .
.
Тому параметри розподілу цих векторів будуть такими:
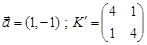 і
і 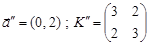 .
.
Дата добавления: 2016-11-02; просмотров: 1473;
