Щільність розподілу ймовірностей n-вимірного закону Гаусса. Незалежність та некорельованість компонент нормально розподіленого вектора.
Означення 19.1. Неперервний випадковий вектор 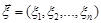 називається гауссівським або нормальним, якщо його щільність розподілу
називається гауссівським або нормальним, якщо його щільність розподілу 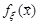 має вигляд
має вигляд
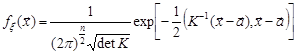 , (19.1)
, (19.1)
де вектор 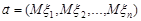 визначає центр розсіювання нормального розподілу в
визначає центр розсіювання нормального розподілу в 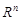 , матриця
, матриця 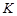 є кореляційною матрицею випадкового вектора
є кореляційною матрицею випадкового вектора 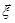 , відповідно
, відповідно 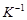 – обернена до неї матриця.
– обернена до неї матриця.
Введемо в евклідовому просторі 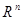 ортонормований базис із власних векторів
ортонормований базис із власних векторів 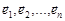 матриці
матриці 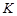 , що відповідає некорельованості компонент гауссівського вектору. Це зробити можливо внаслідок симетричності матриці. Кореляційна матриця
, що відповідає некорельованості компонент гауссівського вектору. Це зробити можливо внаслідок симетричності матриці. Кореляційна матриця 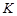 в цьому базисі набуває діагонального вигляду, де на головній діагоналі стоять власні значення матриці
в цьому базисі набуває діагонального вигляду, де на головній діагоналі стоять власні значення матриці 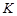 :
:
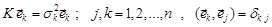 ,
,
де 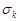 – стандартне відхилення компоненти
– стандартне відхилення компоненти 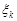 ,
, 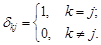 .
.
Отже,
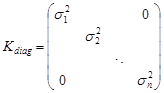 ,
,
визначник кореляційної матриці в цьому базисі дорівнює 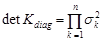 , оберненою до матриці
, оберненою до матриці 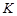 буде матриця
буде матриця
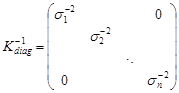 .
.
Тоді скалярний добуток у формулі (19.1) розписується так:
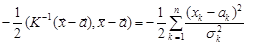 .
.
Щільність розподілу нормально розподіленого вектора 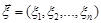 набуває вигляду
набуває вигляду
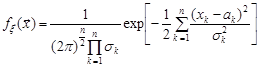 . (19.2)
. (19.2)
Неважко зрозуміти, що права частина формули (19.2) співпадає з добутком щільностей розподілу окремих компонент 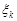 , які мають розподіл Гаусса з параметрами
, які мають розподіл Гаусса з параметрами 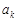 та
та 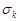 відповідно. Тобто
відповідно. Тобто 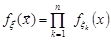 , де
, де 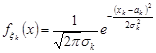 . Це означає незалежність у сукупності випадкових величин
. Це означає незалежність у сукупності випадкових величин 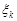 ,
, 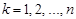 .
.
Отже, якщо координати гауссівського випадкового вектора попарно некорельовані, то вони будуть незалежними у сукупності, тобто для координат гауссівського вектору поняття незалежності та некорельованості рівносильні.
Приклад 19.1. Знайти розподіл довжини гауссівського вектора 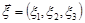 , центр розсіювання якого співпадає з початком координат і кореляційна матриця має вигляд
, центр розсіювання якого співпадає з початком координат і кореляційна матриця має вигляд
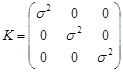 .
.
Розв’язання. Виходячи з умови задачі та формули (19.2), щільність розподілу гауссівського вектора 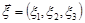 має вигляд
має вигляд
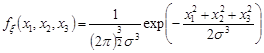 .
.
Введемо випадкову величину 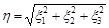 . Для знаходження розподілу цієї величини необхідно знайти ймовірність події
. Для знаходження розподілу цієї величини необхідно знайти ймовірність події 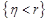 , де
, де 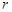 – дійсне число. Зрозуміло, що
– дійсне число. Зрозуміло, що 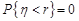 , якщо
, якщо 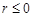 . Нехай
. Нехай 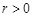 . Використаємо властивість 7 щільності розподілу неперервного випадкового вектора:
. Використаємо властивість 7 щільності розподілу неперервного випадкового вектора:
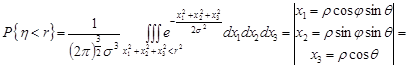
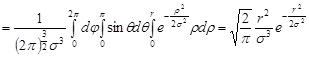 .
.
Отже, функція розподілу довжини випадкового вектора 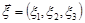 має вигляд
має вигляд
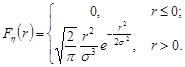
Цей розподіл називається розподілом Максвела.
Приклад 19.2. Щільність розподілу ймовірностей нормально розподіленого вектора 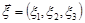 має вигляд
має вигляд
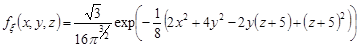 .
.
Записати кореляційну матрицю цього вектора та знайти геометричне місце точок, для яких щільність розподілу ймовірностей дорівнює 0,01.
Розв’язання. Із вигляду даної щільності розподілу випадкового вектора 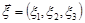 випливає
випливає
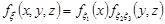 ,
,
де 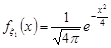 ,
,
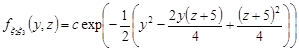 .
.
Порівнюючи ці функції з функціями, що задають щільності розподілів ймовірностей одновимірного та двовимірного законів Гаусса, маємо
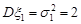 ,
, 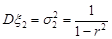 ,
, 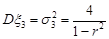 ,
,
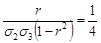 ,
, 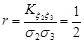 ,
, 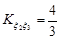 ,
, 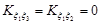 .
.
Отже, кореляційна матриця має вигляд
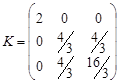 .
.
Для перевірки отриманого результату знайдемо коефіцієнт щільності розподілу
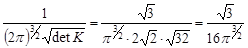 .
.
Геометричним місцем точок із постійною щільністю розподілу ймовірностей 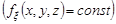 є поверхня еліпсоїда
є поверхня еліпсоїда
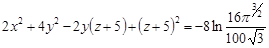 .
.
У випадку незалежності компонент нормально розподіленого випадкового вектора 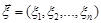 можна знайти ймовірність попадання випадкової точки
можна знайти ймовірність попадання випадкової точки 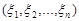 в n-вимірний прямокутний паралелепіпед із сторонами, які паралельні координатним осям, використовуючи функцію Лапласа:
в n-вимірний прямокутний паралелепіпед із сторонами, які паралельні координатним осям, використовуючи функцію Лапласа:
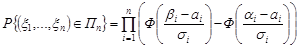 ,
,
де 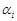 ,
, 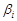 – координати границь прямокутного n-вимірного паралелепіпеда в напрямі вісі
– координати границь прямокутного n-вимірного паралелепіпеда в напрямі вісі 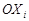
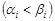 ,
, 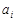 та
та 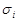 – параметри випадкової компонент
– параметри випадкової компонент 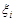 .
.
Дата добавления: 2016-11-02; просмотров: 789;
