ІІІ.7. Принцип максимуму для гармонічної функції.
Принцип максимуму формулюється наступним чином.
Якщо задана функція, яка є гармонічною у області 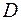 , що обмежена поверхнею
, що обмежена поверхнею 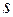 , то своїх екстремальних значень ця функція дістає тільки на границі області.
, то своїх екстремальних значень ця функція дістає тільки на границі області.
Для того, щоб довести зформульований вище тезис максимуму, доведемо попереднью лему.
Лема. Будь-який розв’язок рівняння Пуасона 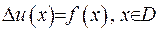 у області
у області 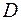 не може сягати свого максимального значення у точці
не може сягати свого максимального значення у точці 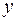 , де
, де 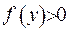 та не може сягати свого мінімального значення у точці
та не може сягати свого мінімального значення у точці 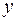 , де
, де 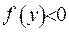 .
.
Доведення. Буде проводитиметься від протилежного. Припустимо, що існує точка 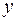 у середині області
у середині області 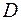 така, що
така, що 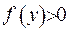 та функція
та функція 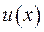 дістає у цієй точці свій максимум
дістає у цієй точці свій максимум 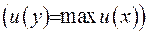 . Отже, випливає, що
. Отже, випливає, що 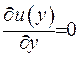 ,
, 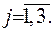 Друга похідна функції має бути від’ємною
Друга похідна функції має бути від’ємною 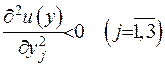 . (цей факт випливає з математичного аналізу, де, як відомо, доведено, що функція, яка сягає максимуму у точці, має у цій точці від’ємну другу похідну), а з цього, у свою чергу, випливає, що
. (цей факт випливає з математичного аналізу, де, як відомо, доведено, що функція, яка сягає максимуму у точці, має у цій точці від’ємну другу похідну), а з цього, у свою чергу, випливає, що 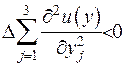 . Тоді як припущено, що у правій частині маємо додатньо визначену функцію
. Тоді як припущено, що у правій частині маємо додатньо визначену функцію 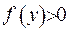 . Отримано суперечність, чим і доведено лему.
. Отримано суперечність, чим і доведено лему.
Застосуємо лему для доведення принципу максимуму.
Нехай 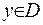 - внутрішня точка області така, що гармонічна функція
- внутрішня точка області така, що гармонічна функція 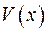 сягає в ній свого максимуму, тобто
сягає в ній свого максимуму, тобто 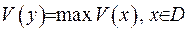 . Це ж саме можна зформульовати так:
. Це ж саме можна зформульовати так: 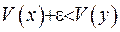 , де
, де  - будь-яка мала величина. Введемо функцію
- будь-яка мала величина. Введемо функцію 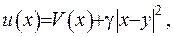 де
де 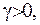
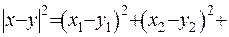
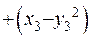 . Виберемо число
. Виберемо число 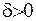 таке, що
таке, що  , та застосуємо до функції
, та застосуємо до функції 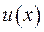 оператор Лапласа:
оператор Лапласа: 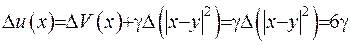 .
.
Виразимо вихідну функцію 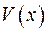 через функцію
через функцію 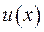 :
: 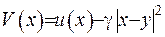 . Оцінимо значення виразу
. Оцінимо значення виразу 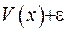 , вибираючи
, вибираючи 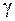 досить малим:
досить малим:
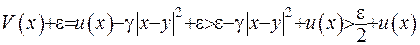 .
.
Виходячи з того, що у точці 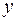 маємо максимум, можна записати:
маємо максимум, можна записати:
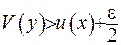 .
.
З іншого боку, так як 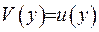 , маємо, що
, маємо, що 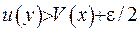 , тобто, у точці
, тобто, у точці 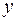 функція
функція 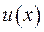 сягає також свого максимуму. Але функція
сягає також свого максимуму. Але функція 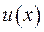 задовольняє рівняння Пуасона
задовольняє рівняння Пуасона 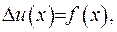 де
де 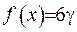 . Як бачимо,
. Як бачимо, 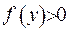 , а з іншого боку,
, а з іншого боку, 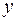 є точка, у якій функція дістає максимум. Відповідно до доведеної вище леми, такий факт не може мати місця. Отже, отримано суперечність, що доводитиме те, що функція може сягати свого мінімального та максимального значення лише на границі області.
є точка, у якій функція дістає максимум. Відповідно до доведеної вище леми, такий факт не може мати місця. Отже, отримано суперечність, що доводитиме те, що функція може сягати свого мінімального та максимального значення лише на границі області.
Слідство 1. Якщо гармонічна функція дорівнює на границі області гармонічності нулеві 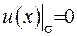 , то вона дорівнює нулеві всюди усередині області.
, то вона дорівнює нулеві всюди усередині області.
Доведення. Доведення проводитиметься від протилежного. Припустимо, що усередині області гармонічності існує точка 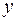 , де функція відмінна від нуля
, де функція відмінна від нуля
-  . Тоді можливі два випадку: або функція у цієї точці додатня, або від’ємна – 1)
. Тоді можливі два випадку: або функція у цієї точці додатня, або від’ємна – 1)  2)
2) 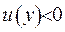 .
.
Відповідно до доведеного вище принципу максимуму у першому випадку функція дістає свого максимуму у точці 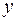 , що розташована усередині області. Прийшли до суперечності з принципом. У другому випадку функція дістає у точці
, що розташована усередині області. Прийшли до суперечності з принципом. У другому випадку функція дістає у точці 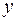 свого мінімального значення, що також є неможливим.
свого мінімального значення, що також є неможливим.
Таким чином, слідство доведено.
Слідство 2. Якщо значення двох гармонічних функцій 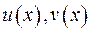 на границі
на границі 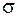 області гармонічності співпадає
області гармонічності співпадає 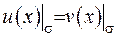 , то вони співпадають і всюди усередині області гармонічності:
, то вони співпадають і всюди усередині області гармонічності: 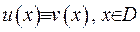 .
.
Доведення. Введемо нову функцію  , тоді на границі області гармонічності функція
, тоді на границі області гармонічності функція  дорівнює нулеві:
дорівнює нулеві:  . Функція
. Функція  задовольняє рівнянню Лапласа -
задовольняє рівнянню Лапласа - 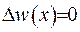 . В силу слідства 1 функція
. В силу слідства 1 функція  дорівнює нулеві всюди усередині області, тобто
дорівнює нулеві всюди усередині області, тобто 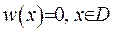 , звідки випливає, що
, звідки випливає, що 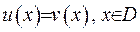 .
.
Дата добавления: 2016-05-05; просмотров: 886;
