ІІІ.10. Інтеграл Гауса.

Відомо формулу для підрахунку похідної за будь-яким

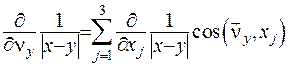(ІІІ.31) Розкриємо похідну під знаком суми:

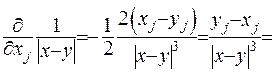
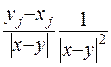. (ІІІ.32)

На відношення 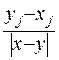можна дивитися, як на відношення катета до гіпотенузи, яке дорівнюватиме .

Співвідношення (ІІІ.32) перепишемо у вигляді

. (ІІІ.33)

Підставимо вираз (ІІІ.33) під знак суми у формулі (ІІІ.31):

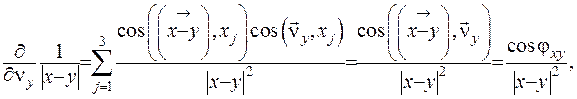
де .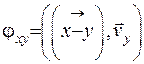

Отже, остаточно отримано

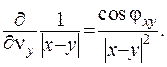(ІІІ.34)

Потенціал подвійного шару прийме вигляд:

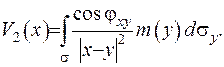(ІІІ.35)

Якщо у формулі (ІІІ.35) взяти 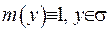, то отримаємо інтеграл Гауса:

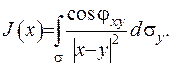(ІІІ.36)

Вважаємо, що - це довільна фіксована точка 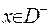, а точка 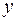- змінна. Тоді зможемо підрахувати важливе співвідношення:

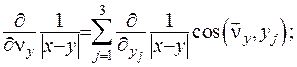
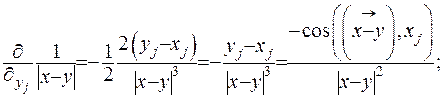
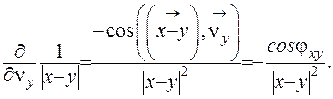
Звідки, враховуючи формулу (ІІІ.36), отримаємо:

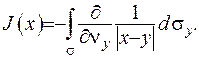(ІІІ.37)

Як відомо, інтеграл по замкненому контуру, що лежить усередині області гармонічності від функції, нормальної похідної дорівнює нулеві. Отже, якщо точка 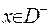, то 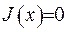. Якщо точка функції належить контуру інтегрування 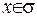, то інтеграл маємо розуміти у невласному сенсі, та збіжним він буде, тільки якщо поверхня є поверхнею Ляпунова.

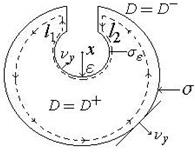Підрахуємо інтеграл Гауса для випадку 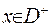, тобто точка лежить усередині області гармонічності. Побудуємо біля точки кулю з центром в

точці , радіуса 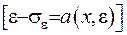так, щоби коло цілком лежало у області гармонічності .

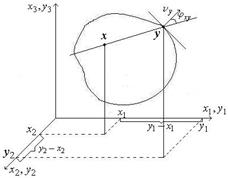
У той часті простору, що лежить за кулею (на рис. ) відповідає заштрихованій області) функція 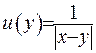є гармоничною. Враховуючи, що замкнені контури та 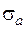повністю лежать у області гармонічності, можна використати теорему про нормальну похідну, записавши рівність

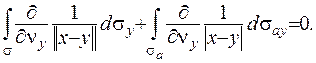(ІІІ.38)

Якщо у точці розташувати початок локальної сферичної системи координат 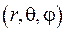, то поверхня 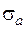у цієї системи координат визначатиметься рівнянням а 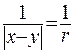. Зовнішня нормаль для області 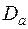на 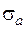буде направлена у напрямок, протилежний напрямку зміни змінної 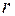. Отже, з цього випливає: 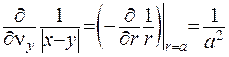. Виходячи з отриманого результату, рівність (ІІІ.38) можна записати наступним чином:

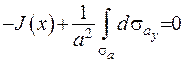(ІІІ.39)

Другий доданок у лівій частині рівності (ІІІ.39) зображує площу кулі та дорівнює 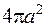. З цього випливає:

(ІІІ.40)

Підрахуємо значення інтегралу 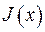при 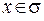. У цьому випадку інтеграл є невласним, і для його підрахування потрібно використати властивості поверхні як ляпуновської. Уникая доведення , приведемо остаточний результат , коли .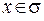

Остаточно маємо

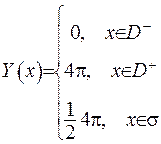(III.41)