Заміна змінних у подвійному інтегралі
Одним із методів спрощення обчислення подвійного інтеграла є метод заміни змінних у подвійному інтегралі.
Нехай у деякій області D  для функції
для функції 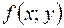
 існує подвійний інтеграл
існує подвійний інтеграл 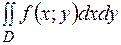 .
.
За допомогою формул:
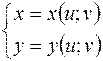
| (1) |
перейдемо до нових змінних u і  v.
v.
Будемо вважати, що формули (1) такі, що нові змінні u і  v визначаються з них єдиним способом:
v визначаються з них єдиним способом:
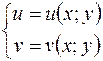
| (2) |
Формули (1) відображають область інтегрування D на площині хОу на області G на площині 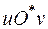 . Формули (2) описують зворотне відображення області G на область D. Таким чином, між точками областей встановлюється взаємно однозначне співвідношення.
. Формули (2) описують зворотне відображення області G на область D. Таким чином, між точками областей встановлюється взаємно однозначне співвідношення.
Справедлива така теорема.
Теорема. Якщо перетворення (1) переводить замкнену обмежену область D в замкнену обмежену область G і є взаємно однозначним, і якщо функції (
1) мають в області G неперервні частинні похідні першого порядку і відмінний від нуля визначник
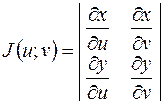 , ,
| (3) |
а функція 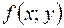 неперервна в області D, то справедлива така формула заміни змінних:
неперервна в області D, то справедлива така формула заміни змінних:
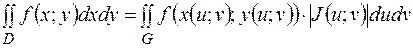 , ,
| (4) |
Функціональний визначник (3) називається визначником Якобі або якобіаном. Таким чином, виконуючи заміну змінних в інтегралі 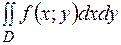 за формулами (1), ми повинні елемент площі
за формулами (1), ми повинні елемент площі 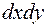 замінити елементом площі
замінити елементом площі 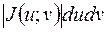 , і стару область інтегрування замінити відповідною їй областю G.
, і стару область інтегрування замінити відповідною їй областю G.
Приклад 1. Обчислити 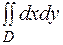
 , якщо область D знаходиться у першій координатній чверті іобмежена кривими
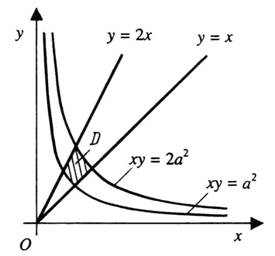
, якщо область D знаходиться у першій координатній чверті іобмежена кривими 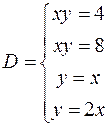 (рис. 2).
(рис. 2).
| 
|
| Рис. 2 | Рис. 3 |
Розв’язання. Перейдемо до нових змінних u і  v за формулами:
v за формулами:
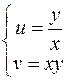 . .
|
Тоді обернене перетворення виглядає так:
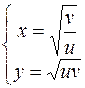 . .
|
Обчислимо якобіан відображення:
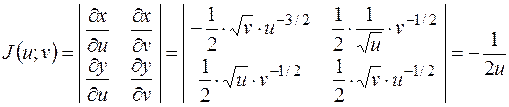 . .
|
Рівняння ліній набувають вигляду 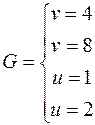
 .
.
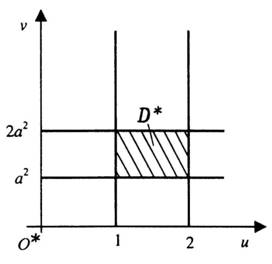
Область D площини хОу перетворюється на прямокутник G площини uО*v (рис. 3).
Застосовуючи формулу (4), дістанемо
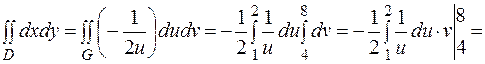
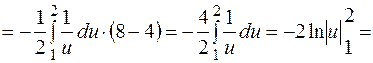
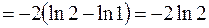 . .
|
Розглянемо заміну декартових координат (x, y)полярними 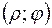 за відомими формулами:
за відомими формулами:
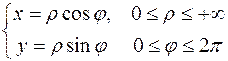 . .
| (5) |
За формулою (3) обчислимо значення якобіана:
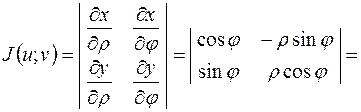
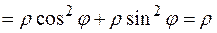 . .
| (6) |
Тоді вираз 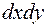 завжди при переході до полярної системи координат треба замінювати на вираз
завжди при переході до полярної системи координат треба замінювати на вираз 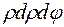 , і формула (4) набуває вигляду:
, і формула (4) набуває вигляду:
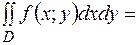
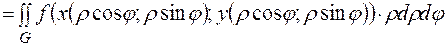 . .
| (4) |
Зауваження. Застосування переходу до полярної системи координат при обчисленні подвійного інтеграла виявляється доцільним, коли
1) область інтегрування обмежена дугами кіл або іншими кривими, що мають прості рівняння у полярній системі координат;
2) підінтегральна функція містить вираз 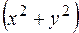 .
.
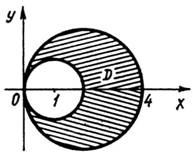 Рис. 4
Рис. 4
| Приклад 2. Обчислити 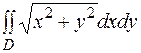 , якщо область D обмежена колами , якщо область D обмежена колами 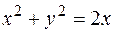 та та 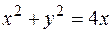 (рис. 4). (рис. 4).
|
Розв’язання. Знайдемо у полярній системі координат рівняння кіл, що обмежують область D:
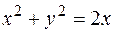 ; ;
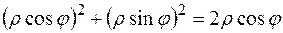 ; ;
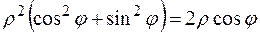 ; ;
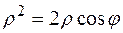 ; ;
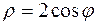 . .
| 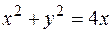 ; ;
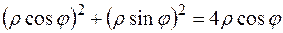 ; ;
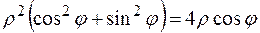 ; ;
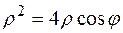 ; ;
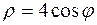 . .
|
Кут 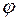 у заданій області змінюється від
у заданій області змінюється від 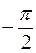 до
до 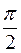 . Змінна
. Змінна 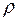 змінюється від
змінюється від 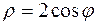 до
до 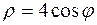 .
.
Підставимо вирази (5) до підінтегральної функції:
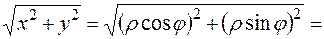
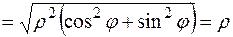 . .
|
Підставимо усі знайдені вирази до заданого інтеграла:
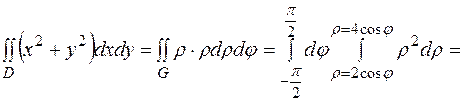
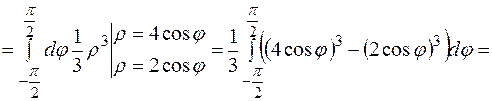
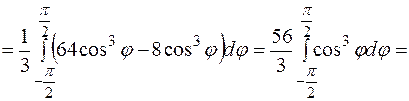
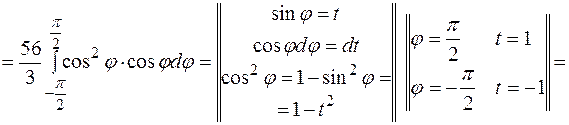
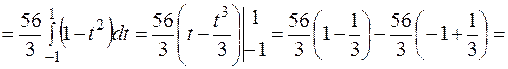
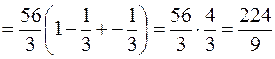 . .
|

| <== предыдущая лекция | | | следующая лекция ==> |
| Совместимость требований пользователей и возможностей отчетности бухгалтерского учета | | | Организация проблемного обучения |
Дата добавления: 2016-10-17; просмотров: 4062;
