Зробимо заміну змінних

,

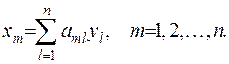де матриця коефіцієнтів 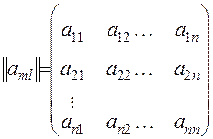є невиродженою, тобто

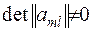. Для неї завжди існує обернена матриця, за допомогою елементів якої нові змінні виражаються через старі

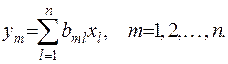(1.7)

(тут і далі будемо опускати знак сумування - ).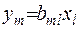

З урахуванням заміни змінних (1.7) нову невідому функцію запишемо як 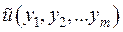. Вона має задовольняти рівняння (1.5). Запишемо похідні через нові змінні:

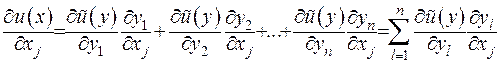(1.8)

Враховуючи, що 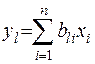, отримаємо 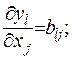тоді

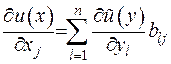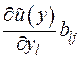= . (1.9)

Остання рівність записана з урахуванням того, що знак сумування опущено.

Звідки друга похідна має подання

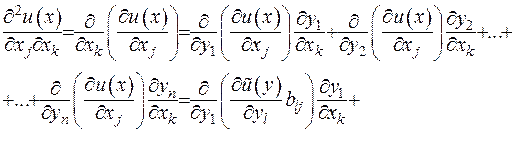
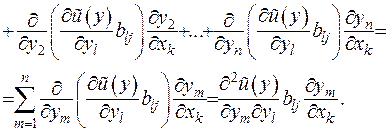
Позначимо 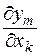як 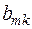, тоді друга похідна буде записана у наступній формі

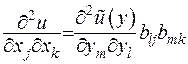. (1.10)

Отже, характеристична частина рівняння

,

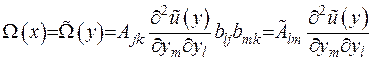або якщо детально

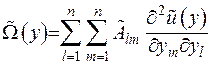, де .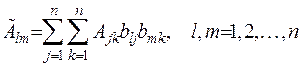

Можна перевірити, що формули перетворення

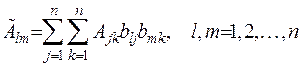
коефіцієнтів при других похідних функції 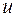під час заміни незалежних змінних відповідно до формул (1.7) збігаються з формулами перетворення коефіцієнтів квадратичної форми

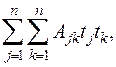(1.11)

Якщо провести в ній лінійне перетворення

,

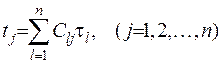то отримаємо вираз

.

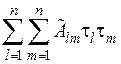У курсі алгебри доведено, що завжди можна підібрати коефіцієнт 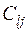таким чином, щоби квадратична форма (1.11) була приведена до суми квадратів, тобто

,

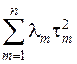Інакше кажучи, 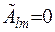, якщо 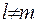та 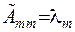. Коефіцієнти 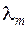або дорівнюватиме 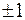, або нулю відповідно.

Отже характеристичну частину рівняння зобразимо у вигляді

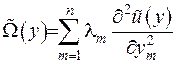. (1.12)

Фактично, вище неявно сформульовано та доведено теорему.

Теорема

Будь-яке квазілінійне рівняння завжди можна привести до канонічного вигляду за рахунок введення нової системи координат, яка отримана зі старої шляхом не вироджених перетворень.

Рішення з характеристичною частиною, що зображується поданням (1.12) називається канонічним.

На основі зображення (1.12) проводиться класифікація рівнянь математичної фізики:

1) якщо всі коефіцієнти 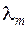однакового знаку, то вихідне рівняння є рівнянням еліптичного типу;

2) якщо існує хоч один коефіцієнт 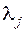, який має знак, протилежний до решти інших, то вихідне рівняння є рівнянням гіперболічного типу;

3) якщо хоч один з коефіцієнтів буде дорівнювати нульові 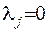, то вихідне рівняння є рівнянням параболічного типу.

У випадку, коли 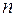дорівнює 2, у виразі (1.11) характеристична частина записується так:

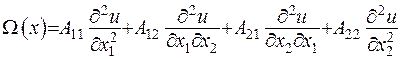(1.13)

Зробимо заміну 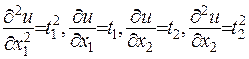. Тоді (1.13) є рівнянням кривої другого порядку

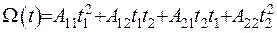
Якщо зробити заміну змінних таку, щоби зникли мішані похідні, наприклад, 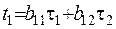, то отримаємо квадратичну форму канонічного вигляду

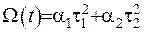
Як відомо з курсу алгебри, з цього випливають рівняння еліпса, гіперболи та параболи, які мають вигляд, відповідний до наступних .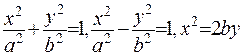

У випадку, коли 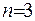, рівняння (1.5) перетворюється на рівняння Лапласа та записується у вигляді

.

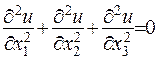Воно є рівнянням еліптичного типу.

Хвильове рівняння

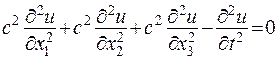
відноситься до рівнянь гіперболічного типу. А рівняння теплопровідності 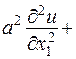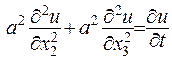- до рівнянь параболічного типу.

Отже, отримано основні класичні рівняння математичної фізики.