ІІІ.8. Основні крайові гармонічні задачі.

Під гармонічними задачами маються на увазі задачі, що пов’язані з рівняннями Лапласа або Пуассона. Їх існує три типа.

Перша основна гармонічна задача (задача Діріхлє) складається з того, що потрібно відшукати гармонічну фунцію усередині області гармонічності, якщо функція задана на границі цієї області.:

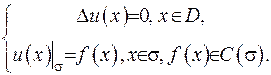(ІІІ.25)

Друга основна гармонічна задача (задача Неймана) – потрібно відшукати значення гармонічної функції усередині області гармонічності, якщо на границі задана нормальна похідна функції:

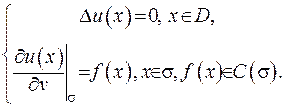(ІІІ.26)

Тут 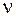- зовнішня нормаль до границі.

Третя основна задача вимагає відшукати значення функції усередині області гармонічності, якщо на границі області задано умови третього роду:

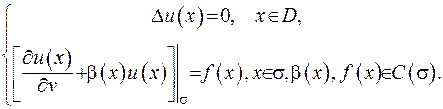(ІІІ.27)

Також розглядаються у математичній фізиці мішані задачі, коли на частині області задано умови одного типу, а на другий її частині – умови іншого типу. Розглянемо деякі властивості задачі Діріхлє.

Теорема: задача Діріхлє завжди має не більше, ніж один розв’язок.

Доведення. Проводимо доведення від протилежного. Нехай існує два розв’язки задачі Діріхлє (ІІІ.25) 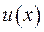та :

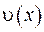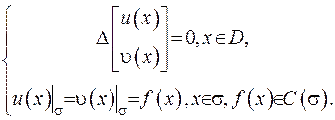(ІІІ.28)

Введемо нову функцію 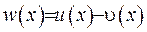. Як бачимо, ця функція задовольняє задачу Діріхлє:

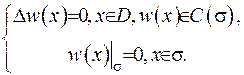(ІІІ.29)

Розв’язок такої задачі - 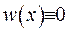. Звідки випливає, що .

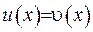Теорема. Задача Діріхлє є стійкою, тобто малим змінам заданих функцій відповідають мали зміни шуканої функції.

Доведення. Нехай маємо, що функції 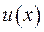та 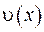задовольняють задачу Діріхлє:

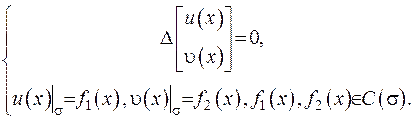
Тоді, якщо виконується, що 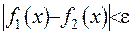, де 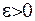як завгодно мале число, то і 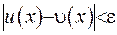. Потрібно довести цей факт.

Введемо нову функцію 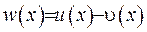. Тоді крайові умови для неї набувають вигляду 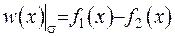. З умови теореми випливає, що

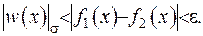(ІІІ.30)

З принципу максимуму випливає, що усередині області значення не можуть бути більшими, ніж на границі. Тобто маємо, що 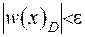. Звідки випливає, що 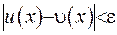, коли .

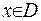Відмітимо, що для другої задачі Неймана довести єдність розв’язку є неможливим. Виходячи з властивості гармонічних функцій, маємо 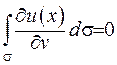. З цього випливає, що для того, щоб задача Неймана була розв’язана, потрібно, щоб виконувалась рівність .

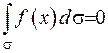Для того, щоб довести коректність задачі Діріхлє, потрібно довести три умови: єдність, стійкість та розв’язуємость задачі. З метою довести цю останню властивість розглянемо деякі додаткові поняття.