Б) Основні факти геометрії Лобачевського.

Оскільки аксіома Лобачевського є запереченням аксіоми паралельності Евкліда, то побудувавши заперечення еквівалентів 5 постулату Евкліда, ми отримаємо твердження, справедливі в геометрії Лобачевського. Наведемо кілька таких тверджень.

Теорема. Перпендикуляр і похила, проведені до однієї прямої в одній площині, не завжди перетинаються.

Доведення. Припустимо супротивне, тобто нехай в площині Лобачевського виконується твердження Лежандра. Але його наслідком є аксіома паралельності Евкліда, що неможливо в аксіоматичній теорії Лобачевського.

Теорема. Існують трикутники, навколо яких не можна описати коло.

Доведення. Аналогічно методом від супротивного, використовуючи еквівалентність твердження Ф. Бойяї та аксіоми паралельності Евкліда.

На практичному занятті буде побудовано трикутник, що задовольняє теоремі, тобто трикутник, навколо якого не можна описати коло.

Теорема. Сума внутрішніх кутів будь-якого трикутника менша за .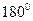

Доведення. За теоремою абсолютної геометрії в кожному трикутнику сума внутрішніх кутів будь-якого трикутника не більша (менша або дорівнює) 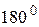. Якщо припустити, що існує хоча б один трикутник, в якому сума внутрішніх кутів дорівнює 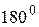, то як наслідок отримаємо, що сума внутрішніх кутів будь-якого трикутника дорівнює 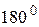. Це твердження є еквівалентним аксіомі паралельності Евкліда, що і говорить про те, що наше припущення невірне. Отже, сума внутрішніх кутів будь-якого трикутника менша за .

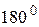Наслідок. Сума внутрішніх кутів опуклого чотирикутника менша за .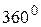

Теорема. Сума внутрішніх кутів трикутника є непостійною величиною.

Доведення. Методом від супротивного проведенням трансверсалі.

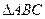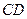, , - транверсаль. 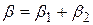, 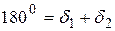як суміжні. Тоді з припущення 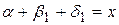, 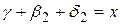. Тоді 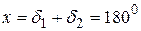, а з іншого боку 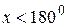за попередньою теоремою.

Означення. Еквідистантою називається множина точок, рівновіддалених від даної прямої.

Теорема. Еквідистанта є кривою.

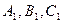Доведення. Розглянемо на еквідистанті 3 різні точки і припустимо, що вони колінеарні. Опустимо з них перпендикуляри на дану пряму і позначимо основи перпендикулярів через відповідно. Отримані чотирикутники 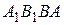, 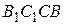і 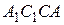є чотирикутниками Саккері. Кути при верхній основі чотирикутника Саккері повинні бути рівними. Отже, 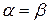і 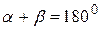як суміжні. Ці рівності дають 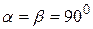, звідки сума внутрішніх кутів опуклого чотирикутника дорівнює 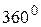, що неможливо в геометрії Лобачевського.

Теорема.Дві розбіжні прямі мають єдиний спільний перпендикуляр, по обидві сторони від якого вони необмежено віддаляються одна від одної.

Теорема (четверта ознака рівності трикутників).Якщо три кути одного трикутника рівні відповідним кутім іншого трикутника, то такі трикутники рівні.

Наслідок.Не існують не конгруентні подібні трикутники. На площині Лобачевського немає відношення подібності фігур.

Теорема.Кут при верхній основі чотирикутника Саккері гострий.

Теорема.Середня лінія трикутника має довжину, меншу за половину довжини основи.

Теорема.Сторона правильного шестикутника більша за радіус описаного кола.

3. Дослідження системи аксіом планіметрії Лобачевського. Інтерпретації Пуанкаре.

Побудуємо модель неевклідової планіметрії на множині об’єктів евклідової площини, що була запропонована А.Пуанкаре. Розглянемо на евклідовій площині деяку пряму 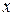(наприклад, горизонтальну). Ця пряма визначає дві півплощини. Одну з них назвемо «верхньою». Будемо називати неевклідовими точками точки верхньої півплощини (без точок прямої 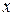), неевклідовими прямими – евклідові півкола, що знаходяться в верхній півплощині та ортогональні до прямої 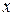(тобто мають центри на прямій 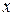), а також евклідові півпрямі, що спираються на пряму 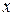та утворюють з нею прямий кут. Ці півпрямі будемо називати півколами нескінченно великого радіусу

Далі визначимо поняття: «точка належить прямій» або «пряма проходить через точку». Нехай 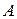– неевклідова точка, 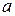– неевклідова пряма, яка є деяким півколом (яке теж будемо позначати буквою 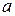). Будемо говорити, що точка 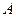знаходиться на (неевклідовій) прямій 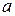, якщо ця точка розташована на евклідовому півколі 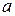в сенсі тих відношень, які мають місце в евклідовій геометрії. Те, що для неевклідових точок та прямих справедливі аксіоми 1.1–1.3, легко перевіряється засобами евклідової геометрії.

Насправді, аксіома 1.1 виконується, оскільки через дві точки 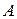і 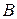верхньої півплощини завжди можна провести півколо, ортогональне до прямої .

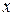Аксіома 1.2 виконується, оскільки два півкола, що зображають неевклідові прямі, можуть мати не більше однієї спільної точки.

Аксіома 1.3. виконується, оскільки на півколі існує нескінченно багато точок і в верхній півплощині існує нескінченно багато точок, що не належать вибраному півколу.

Далі визначимо поняття «лежати між» по відношенню до неевклідових точок на неевклідових прямих. Нехай 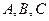– три точки неевклідової прямої, яка зображується півколом 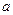. Будемо говорити, що точка 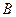(в неевклідовому сенсі) лежить між точками 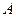і 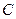, якщо на півколі 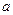вона розташована між точками 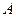і 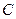в тому сенсі, як це розуміється в евклідовій геометрії . Інакше кажучи, порядок точок на неевклідовій прямій співпадає з порядком точок на евклідовому півколі, що зображає цю пряму в верхній півплощині.

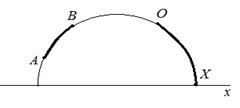Тому неевклідів відрізок 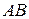зображується дугою півкола з кінцями 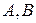; неевклідова півпряма, що виходить з точки 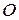, зображується дугою 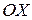, кінець 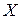якої знаходиться на прямій 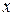. Точка 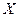при цьому не повинна зараховуватись до точок неевклідової півпрямої.

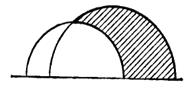
Неевклідовим кутом будемо називати сукупність двох неевклідових півпрямих, що виходять з однієї неевклідової точки.

В цій моделі роль рухів відіграють інверсії з центрами на прямій 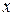. Тому для неозначуваного поняття «конгруентність» дамо такі означення.

Назвемо неевклідів відрізок 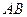конгруентним неевклідову відрізку 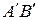, якщо існує така послідовність інверсій, що їх добуток відображає евклідову кругову дугу 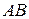в кругову дугу .

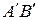Аналогічно, назвемо неевклідів 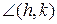конгруентним неевклідовому куту 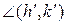, якщо існує така послідовність інверсій, що їх добуток відображає сторони першого кута на сторони другого кута.

Можна перевірити, що аксіоми другої, третьої та четвертої груп теж виконуються.

Перевіримо, чи виконується на цій моделі аксіома Лобачевського.

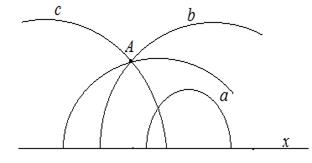Візьмемо будь-яке півколо 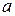верхньої півплощини, ортогональне до прямої 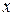(неевклідову пряму). Нехай 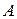– деяка точка верхньої півплощини, яка не належить цьому півколу. Легко перевірити що через точку 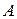проходить нескінченно багато різних півкіл, ортогональних до прямої 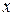, які не мають спільних точок з півколом 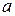. Іншими словами можна сказати: через довільну неевклідову точку, що лежить поза даною неевклідовою прямою, проходить нескінченно багато різних неевклідових прямих, які не перетинають дану пряму. Отже, в системі об’єктів, що розглядаються, має місце постулат Лобачевського. Таким чином, ця система представляє собою модель геометрії Лобачевського.